(R) Odds ratio 메타분석 실습 (코드 리뷰)

독립된 실험으로부터 산출된 Odds ratio 들을 메타분석으로 통합해봅시다.

 

연구를 수행할 때 모든 병원들의 데이터를 합쳐서 한꺼번에 분석을 수행하면 참 좋겠지만, 아무래도 개인정보와 관련된 제도적인 한계와 각 병원의 데이터 가치에 따른 이해관계에 의해 raw 데이터를 합치는 것은 어려운 일입니다.

 

따라서 각 병원들에서 따로 수행한 결과들을 합쳐서, 통계적으로 유의한 종합 결과를 가져오는 메타분석을 수행하게 됩니다.

메타분석은 odds ratio, risk ratio, hazard ratio 등의 statistic에 적용할 수 있습니다. 이번 포스팅에서는 odds ratio의 결과들을 어떻게 메타분석으로 합치는지 살펴볼 것입니다. odds ratio에 대한 내용은 [Odds ratio & Confidence interval 계산 방법] 에서 살펴보시기 바랍니다.

 

본 포스팅에서는 R의 "metafor" 패키지를 활용합니다.

 

참고자료: https://www.metafor-project.org/doku.php/tips:assembling_data_or

Assembling Data for a Meta-Analysis of (Log) Odds Ratios [The metafor Package]

 

 

 Data Representation

 

데이터를 불러와봅시다.

library(metafor)
dat.bcg

 

dat.bcg는 metafor 패키지 안에 있는 데이터셋입니다. 총 13개의 독립된 실험 결과를 가지고 있습니다.

여기서 tpos, tneg, cpos, cneg 네 가지 컬럼을 활용할 것입니다.

 

• tpos: Target Positive, 실험군에서 Positive인 대상 수
• tneg: Target Negative, 실험군에서 Negative인 대상 수
• cpos: Comparator Positive, 대조군에서 Positive인 대상 수
• cneg: Comparator Negative, 대조군에서 Negative인 대상 수

 

 

 

 

 Odds Ratio

 

위에서 소개한 네 가지 항목으로 Odds ratio를 간단히 계산할 수 있습니다. 첫 번째 예시를 2x2 테이블로 가져와봅시다.

 

	Positive	Negative
Target	tpos; 4	tneg; 119
Comparator	cpos; 11	cneg; 128

 

여기서 log odds ratio와 log odds ratio의 표준오차(Standard Error) 계산식은 다음과 같습니다.

$$\text{Odds ratio} = \ln{\frac{ \frac{\text{tpos}}{\text{tneg}} }{ \frac{\text{cpos}}{\text{cneg}} }} = \ln{\frac{ \frac{4}{119} }{ \frac{11}{128} }} = \ln{0.3911} = -0.9387 $$

$$\text{SE} (\log{OR}) = \sqrt{\frac{1}{\text{tpos}} + \frac{1}{\text{tneg}} + \frac{1}{\text{cpos}} + \frac{1}{\text{cneg}}} = \sqrt{\frac{1}{4} + \frac{1}{119} + \frac{1}{11} + \frac{1}{128}} = \sqrt{0.3571} = 0.5976$$

 

metafor 패키지에서는 log odds ratio로 메타분석을 수행하기 때문에 log로 계산을 해보았습니다. 

 

metafor 패키지의 "escalc" 함수는 tpos, tneg, cpos, cneg 네 가지 항목을 활용하여, 메타분석에서 활용할 odds ratio와 표준오차를 간단히 계산해줍니다. 다음 코드를 봅시다.

 

escalc(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg)
dat1 <- escalc(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.bcg)

 

yi 항목이 log odds ratio에 해당하고, vi는 분산(표준오차의 제곱)에 해당합니다. 위에서 직접 계산했던 값과 잘 일치하는 것을 확인할 수 있습니다.

 

 

 

 

 Meta Analysis

 

메타분석을 수행하는 코드는 다음과 같습니다.

res1 <- rma(yi, vi, data=dat1)
res1

 

"rma" 함수를 사용하면 자동으로 Random-Effect 메타분석 모델을 리턴하고, Heterogeneity를 계산하는 값으로 tau, $I^2$, $H^2$을 보여줍니다. 이 Heterogeneity를 보고 이후 분석 방향을 사용자가 결정할 수 있습니다.

 

산출된 값들은 "$" 을 붙여서 추출할 수 있습니다.

 

 

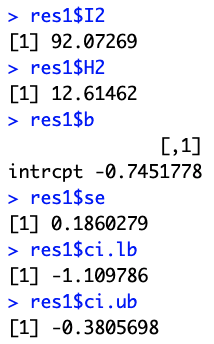
Heterogeneity가 너무 낮아 Fixed Effect 모델을 리턴하고 싶다면 다음과 같이 설정해주면 됩니다.

res1 <- rma(yi, vi, data=dat1, method="FE")
res1

 

 

---

 

여기까지 odds ratio의 메타분석 실습을 살펴보았습니다. 개인적으로 아래와 같은 유의사항이 있을 것 같습니다.

 

* metafor 패키지는 rma 함수 사용 시에, vi 컬럼에 표준오차가 아닌 분산이 들어간다는 점을 유의해야 합니다.

* rma로 산출된 odds ratio, 신뢰구간은 log가 씌워진 값이기 때문에, 일반 수치로 가져오고 싶다면 exp를 씌워주어야 합니다.

 

 

감사합니다!