| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- XGBoost
- lime
- data science
- Explainable AI
- Machine Learning
- Gradient Tree Boosting
- Back-propagation
- deep learning
- Gradient Boosting Machine
- Today
- Total
Kicarussays
(Statistics, R) 기술적 통계분석 루틴 (1) : 범주형 종속변수 본문
데이터 분석을 진행하다보면 그룹 간의 차이를 규명하기 위해 통계 분석 기법을 사용하게 됩니다. 상황에 맞는 여러 기법들이 있고, 해당 기법들이 그 상황에 맞는 것을 수학적으로 증명할 수도 있습니다. 하지만 저와 같은 비전공자들은 "기술적으로" 올바른 통계 기법들을 사용하는 것이 당장 필요한 작업인 경우가 많습니다.
본 포스팅은 "기술적으로" 올바른 통계 분석 기법을 선택하여 사용하는 방법을 정리하고자 시작하게 되었습니다. 최종 목표는 다음과 같습니다.
Goal. 상황에 맞는 통계 기법을 선택하고 해당 통계 기법을 R로 구현한다.
확률 변수, 확률 분포, 기댓값, 검정통계량 등 기초적인 통계 개념을 알고 있다는 전제 하에 포스트를 작성하였습니다. "기술적으로" 통계 분석을 하는 방법에 대한 내용인 만큼 개념적인 부분은 대부분 생략하였음을 밝힙니다.
먼저 아래 플로우차트를 보겠습니다. (출처: m.blog.naver.com/y4769/220024117776)

통계 분석 기법 선택의 흐름을 한 눈에 볼 수 있네요. 사실 이 범주에서 벗어난 케이스는 거의 없는 것 같습니다. 이 경우들에 대해서 모든 기법을 구현하고 결과를 해석할 수 있다면 통계 분석을 "도구"로 사용하는 데에는 큰 지장이 없을 것입니다. 이번 포스팅에서는 범주형 종속 변수의 경우를 보기로 하고, 상위 개념부터 살펴보도록 하겠습니다.
종속 변수(Y변수) : 연속형 / 범주형
처음으로 종속 변수가 연속형인지 범주형인지 판단해야 합니다.
- 종속 변수: 연구자들이 어떻게 변하는지 알고 싶어하는 변수
데이터 분석에서는 클래스(label)로 말할 수 있을 것 같습니다. 예를 들어 맹장수술을 한 환자군에서 복막염 동반 여부를 예측하고자 한다고 해봅시다. 클래스로 선정하고 여부에 따라 1과 0을 부여하였다면, 이 복막염 동반 여부가 종속 변수가 되는 것입니다. - 연속형 / 범주형 변수
연속형: 길이, 전류, 압력, 온도, 시간처럼 실수(Real number)로 나타낼 수 있는 종류의 변수
범주형: 꽃잎의 수, 불량의 개수, 복막염 동반 여부 등 정수(Integer)로 나타낼 수 있는 종류의 변수
이어서 독립 변수의 특성을 판단합니다.
독립 변수(X변수) : 범주형 / 연속형 or 독립 변수가 2개 이상
- 독립 변수: 연구자가 의도적으로 변화시키는 변수
데이터에서 특성(Feature)에 해당하는 변수입니다. 예를 들어, 환자의 특성이나 환경에 따라서 복막염 동반 여부가 달라질 수 있을 것입니다. 이 때 환자의 특성이나 환경이 독립 변수가 되는 것입니다.
드디어 첫 번째 케이스를 발견했습니다. 종속 변수와 독립 변수가 모두 범주형이고, 독립 변수가 하나일 때 카이제곱 분석(Chi-squared analysis)을 사용합니다. 위의 플로우차트에서 확인할 수 있습니다. 예를 한 번 들어보면서 시작해볼까요?
1. 카이제곱 분석 (= 카이제곱 검정, Chi-square test)
남녀간의 흡연 여부에 차이가 있는지 분석하고자 한다고 가정합시다. 이 때, 종속변수는 흡연 여부가 될 것이고, 독립 변수는 성별이 되겠네요. 성별과 흡연 모두 범주형 변수이니, 이 케이스에는 카이제곱 검정을 실시하면 됩니다.
여기서 헷갈릴 수 있는 것이, 지금 든 예시의 범주형 변수는 남자/여자, 흡연/비흡연으로 2가지 경우가 있지만, 경우가 여러개인 범주형 변수에도 카이제곱 분석을 사용할 수 있습니다. 독립 변수가 2개 이상일 때 카이제곱 분석을 사용할 수 없는 것이고, 범주형 변수의 경우의 수에 관계 없이 카이제곱 분석을 할 수 있습니다.
다시 예시로 돌아와서, 표로 한번 예시를 정리해봅시다.
| 흡연 | 비흡연 | |
| 남자 | $N_1$ | $N_2$ |
| 여자 | $N_3$ | $N_4$ |
위와 같은 경우에 카이제곱 검정을 사용하는 것입니다. 검정 결과에 따라 남녀간의 흡연 여부 차이가 유의미한지 판단할 수 있습니다.
R에서 카이제곱 검정을 하는 과정을 살펴봅시다.
|
1
2
3
4
5
6
7
8
9
10
11
|
# 카이제곱 검정 실습
man = c(300, 700)
woman = c(30, 970)
dat = data.frame(rbind(man, woman))
names(dat) = c("smoking", "non-smoking")
chisq.test(dat)
|
cs |
다음 코드의 실행 결과는 아래와 같습니다. 남자 1000명 중 흡연자는 300명, 여자 1000명 중 흡연자는 30명으로 설정하고 카이제곱 검정을 실행하였습니다.
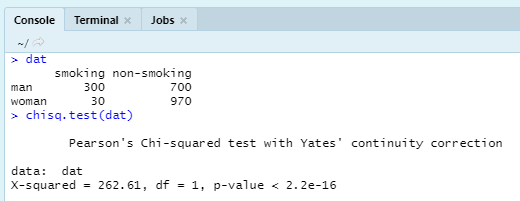
실행 결과, p-value가 매우 작은 것을 볼 수 있습니다. 이를 통해서 성별 간의 흡연 여부 차이가 있는 것으로 결론지을 수 있습니다.
2. (순서형, 명목형)로지스틱 회귀분석 (Logistic Regression; ordinal, multinomial)
종속 변수가 범주형이고, 독립 변수가 범주형 변수 하나가 아닌, 연속형이거나 둘 이상일 때 로지스틱 회귀분석을 수행합니다. 이분형 로지스틱 회귀분석은 종속 변수의 범주가 2개인 경우, 다중명목형(Multinomial)은 종속 변수의 범주가 3개 이상인 경우, 순서형(Ordinal)은 종속 변수가 서열을 나타낼 때 사용합니다.
R에서 실행해보면서 각 회귀분석들을 살펴보도록 합니다.
1. 이분형 로지스틱 회귀분석
제가 작업중인 데이터셋을 가져왔는데, 청소년들의 성별에 따라 키와 몸무게가 다른지 보려고 합니다. 아래는 전체 코드입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# 로지스틱 회귀분석 실습
library(dplyr)
setwd("D:/Dream/SNUH_BMI/CDM-graves_disease")
data = read.csv("GD_EMR.csv")
clinical_data = data %>%
select(c("snuh_id", "sex", "snu_height", "snu_weight")) %>%
na.omit()
clinical_data = clinical_data %>%
mutate(gender = ifelse(sex == "F", 1, 0))
logistic = glm(gender~snu_height+snu_weight, family=binomial, data=clinical_data)
summary(logistic)
|
cs |
데이터셋 모양은 다음과 같습니다.

R에서 이분형 로지스틱 회귀분석을 수행할 때에는, 독립변수의 값을 0 또는 1로 설정해주어야 합니다. 따라서 11번 줄에서 "F", "M"으로 되어 있는 성별(sex)을 gender 컬럼에 다시 만든 것을 볼 수 있습니다.
로지스틱 회귀분석 실행 결과는 다음과 같습니다.
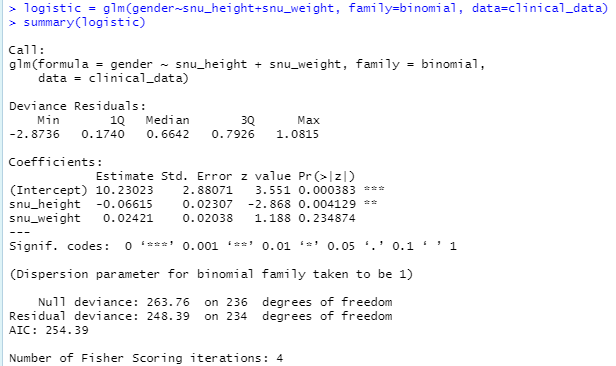
보시면 snu_height의 p값은 매우 작고, snu_weight의 p값은 꽤 크게 나온 것을 볼 수 있습니다. 이 결과를 통해, 제가 가지고 있는 데이터셋에서 성별에 따라 키에는 차이가 있지만, 몸무게는 차이가 없다는 결론을 내릴 수 있습니다.
2. 다중명목형 로지스틱 회귀분석
다른 데이터셋을 사용해 보겠습니다. survival 패키지에 있는 colon 데이터를 가져왔습니다. 전체 코드는 아래와 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# 다중명목형 로지스틱 회귀분석 실습
library(dplyr)
library(survival)
library(nnet)
# 종속변수: status(대장암 재발 또는 사망인 경우 1 아니면 0)
# 독립변수:
# sex: 성별
# rx: 치료 종류
# obstruct: 종양에 의한 장의 폐쇄
# perfor: 장의 천공
# adhere: 인접장기와의 유착
# nodes: 암세포가 확인된 림프절 수
# differ: 암세포의 조직학적 분화 정도
# extent: 암세포가 침습한 깊이
data = na.omit(colon)
result = multinom(formula = rx ~ sex+age+obstruct+perfor+adhere+nodes+differ+extent, data=data)
summary(result)
z = summary(result)$coefficients / summary(result)$standard.errors
(1 - pnorm(abs(z), 0, 1)) * 2
|
cs |
데이터 형식은 다음과 같습니다.
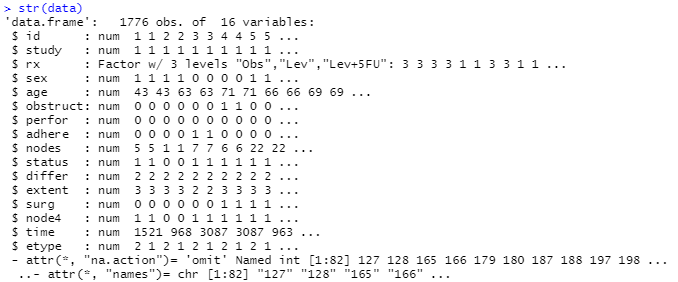
nnet 라이브러리의 multlinom 함수를 사용했는데, formula에 종속변수 ~ 독립변수들 값을 넣어줍니다(19번째 줄).
저는 rx를 종속변수로 설정하였고, sex, age, obstruct, perfor, adhere, nodes, differ, extent를 독립변수로 설정하였습니다. rx는 총 3개의 범주(Obs, Lev, Lev+5FU)를 갖는데, 첫 번째 범주를 기준으로 결과가 나오게 됩니다.
그리고 summary를 실행한 결과는 다음과 같습니다.
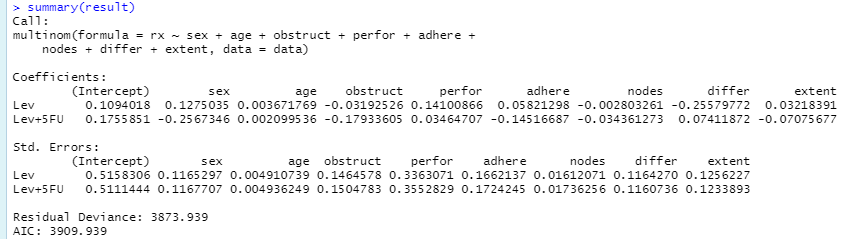
결과에 Obs범주가 없죠? 첫 번째 범주를 기준으로 결과가 나와서 그렇습니다. 결과 일부를 해석해보면, sex가 0(남자)에서 1(여자)로 될 때, $\log \frac{P(rx = Lev)}{P(rx = Obs)}$ 값이 0.1275 만큼 증가한다는 뜻입니다. 저 숫자들은 각 변수들에 해당하는 계수가 되는 것이죠.
data$rx <- relevel(data$rx, ref = "Lev") 이 코드로 기준을 Obs에서 Lev로 바꿀 수도 있습니다.
이제 각 계수들이 유의미한지 p값을 산출하여 확인해보도록 하겠습니다. 계수가 0이라는 귀무가설 하에서, coef~N(0, sd^2)인 것을 이용하겠습니다(22, 23번 줄).

각 변수들의 p값이 산출된 결과입니다. Obs와 Lev를 구분하는 데에는 differ가, Obs와 Lev+5FU를 구분하는 데에는 sex, nodes가 유의미한 변수라고 결론을 내릴 수 있겠네요.
3. 순서형 로지스틱 회귀분석
방금 전의 코드에서 종속변수 rx를 다중명목형이 아닌, 순서형으로 가정하고 회귀분석을 진행해 보겠습니다. 전체 코드는 아래와 같습니다.
|
1
2
3
4
5
6
7
8
|
# 순서형 로지스틱 회귀분석 실습
library(MASS)
library(AER)
m = polr(rx ~ sex+age+obstruct+perfor+adhere+nodes+differ+extent, data=data, Hess=T)
summary(m)
coeftest(m)
|
cs |
MASS 패키지의 polr 함수로 순서형 로지스틱 회귀분석을 하고, AER 패키지의 coeftest를 이용하여 쉽게 p값을 계산할 것입니다. 이전에는 직접 p값을 계산했지만 coeftest를 통해서 보다 쉽게 계수들의 p값을 계산할 수 있습니다. 실행 결과는 다음과 같습니다.
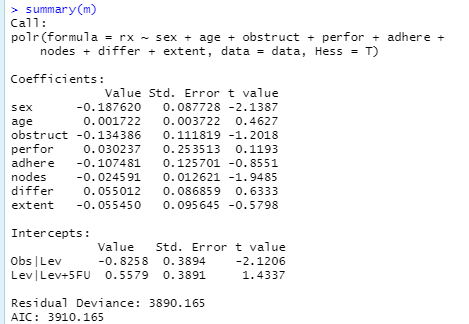
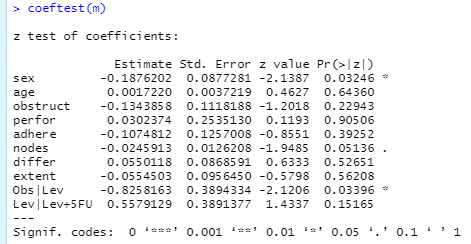
결과를 보면 sex, nodes의 p값이 유의하게 나오는 것을 통해, 이 변수들이 종속변수에 영향을 주는 요소라고 판단할 수 있습니다. 보다 자세한 결과 해석은 다음 링크에서 확인하실 수 있습니다.
출처: 3months.tistory.com/236, 3months.tistory.com/245, m.blog.naver.com/y4769/220024117776, stats.idre.ucla.edu/r/faq/ologit-coefficients/
'Statistics (R)' 카테고리의 다른 글
| (R) Odds ratio 메타분석 실습 (코드 리뷰) (0) | 2022.02.03 |
|---|---|
| Odds ratio & Confidence interval 계산 방법 (0) | 2021.10.22 |
| Calibration Plot 설명 (0) | 2021.08.11 |
| (Statistics, R) 기술적 통계분석 루틴 (2) : 연속형 종속변수 (0) | 2020.12.28 |
| (R) rread_csv 파라미터 정리 및 parsing failure 해결 방법 (0) | 2020.08.26 |



