| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Explainable AI
- Gradient Boosting Machine
- Gradient Tree Boosting
- lime
- deep learning
- Back-propagation
- data science
- Machine Learning
- XGBoost
- Today
- Total
Kicarussays
(Statistics, R) 기술적 통계분석 루틴 (2) : 연속형 종속변수 본문
저번 "기술적 통계분석 루틴 (1) : 범주형 종속변수" 포스트에 이어서 이번 포스트에서는 연속형 종속변수를 가진 데이터에 대하여 설명해볼까 합니다.
다시 한번 목표와 통계 분석 기법 플로우차트를 상기해보도록 하겠습니다.
Goal. 상황에 맞는 통계 기법을 선택하고 해당 통계 기법을 R로 구현한다.
저번 포스팅에서 가져온 통계분석 기법 플로우차트입니다. (출처: m.blog.naver.com/y4769/220024117776)

종속 변수(Y변수) : 연속형 / 범주형
처음으로 종속 변수가 연속형인지 범주형인지 판단해야 합니다.
- 종속 변수: 연구자들이 어떻게 변하는지 알고 싶어하는 변수
데이터 분석에서는 클래스(label)로 말할 수 있을 것 같습니다. 예를 들어 맹장수술을 한 환자군에서 복막염 동반 여부를 예측하고자 한다고 해봅시다. 클래스로 선정하고 여부에 따라 1과 0을 부여하였다면, 이 복막염 동반 여부가 종속 변수가 되는 것입니다. - 연속형 / 범주형 변수
연속형: 길이, 전류, 압력, 온도, 시간처럼 실수(Real number)로 나타낼 수 있는 종류의 변수
범주형: 꽃잎의 수, 불량의 개수, 복막염 동반 여부 등 정수(Integer)로 나타낼 수 있는 종류의 변수
본 포스트에서는 종속변수가 연속형인 경우를 다룹니다.
독립 변수(X변수) : 범주형 / 연속형
- 독립 변수: 연구자가 의도적으로 변화시키는 변수
데이터에서 특성(Feature)에 해당하는 변수입니다. 예를 들어, 환자의 특성이나 환경에 따라서 복막염 동반 여부가 달라질 수 있을 것입니다. 이 때 환자의 특성이나 환경이 독립 변수가 되는 것입니다.
위의 플로우차트를 토대로 기법들을 하나하나 살펴보도록 하겠습니다.
1. 선형회귀분석(단순회귀분석 & 다중회귀분석)
가장 기초적인 통계분석 기법 중 하나입니다. 단순회귀분석의 간단한 예를 들어보자면, 종속 변수가 사람의 키, 독립 변수가 사람의 나이일 때를 생각해볼 수 있겠네요.
다른 분석들과 마찬가지로 선형회귀분석 또한 가정들을 충족해야 신뢰성있는 결과를 도출할 수 있습니다. 선형회귀분석에는 네 가지 기본가정이 있습니다.
- 선형성(Linear Relationship)
- 종속변수와 독립변수간의 선형성을 만족하는 특성
- 가정을 만족하는지 확인하는 방법
- 산점도(scatter plot)를 그려서 시각적으로 확인 - 가정이 위배되었을 때 대안
- 독립 / 종속 변수의 비선형 변환을 통해서 선형성을 보이게끔 데이터를 조정합니다.
- 다른 독립변수를 추가하여 선형성을 보이게끔 데이터를 조정합니다.
- 종속변수와 독립변수간의 선형성을 만족하는 특성
- 독립성(Independence)
- 독립변수 간에 독립성을 만족하는 특성 (잔차가 독립적인 특성)
- 가정을 만족하는지 확인하는 방법
- VIF, Durbin-Watson 검정을 통해서 확인
- VIF는 10 이상일 경우 다중공선성이 있다고 판단하고, 5가 넘으면 주의할 필요가 있는 것으로 보는 편입니다.
- Durbin-Watson 검정의 귀무가설은 잔차가 독립적이지 않다는 것입니다. 따라서 해당 검정의 p-value가 유의수준보다 클 경우 독립성을 만족하는 것으로 판단할 수 있습니다. - 가정이 위배되었을 때 대안
- 적절한 변수선택법을 사용하여 연관이 강한 변수를 제거해주어야 합니다.
- 독립변수 간에 독립성을 만족하는 특성 (잔차가 독립적인 특성)
- 등분산성(Homoscedasticity)
- 잔차(예측값과 본래 데이터의 값의 차이)가 특정한 패턴 없이 고르게 분포되어 있는 특성
- 가정을 만족하는지 확인하는 방법
- Residual vs Fitted Plot을 통해 확인합니다. - 가정이 위배되었을 때 대안
- 종속 변수를 변환합니다.
- 가중선형회귀분석(Weighted Linear Regression) 기법을 이용합니다. 이 기법은 다음 번에 자세히 다뤄보도록 하겠습니다.
- 잔차(예측값과 본래 데이터의 값의 차이)가 특정한 패턴 없이 고르게 분포되어 있는 특성
- 정규성(Normality)
- 잔차가 정규성을 만족하는 특성
- 가정을 만족하는지 확인하는 방법
- Normal Q-Q Plot을 통해 시각적으로 확인합니다.
- Shapiro-Wilk, Kolmogorov-Smirnonov 검정 등의 기법을 사용할 수 있지만, 이러한 검정 기법들은 샘플의 사이즈가 클 때 해당 샘플이 정규성을 만족하지 않는다고 결론을 내는 경향이 있습니다. - 가정이 위배되었을 때 대안
- 이상치들이 큰 영향을 미치고 있는지 확인하고 제거합니다.
- 변수변환을 시도해볼 수 있습니다.
- 잔차가 정규성을 만족하는 특성
선형회귀분석을 수식으로 나타내면 다음과 같습니다. $$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_n X_n + \epsilon$$
각 $\beta$의 값이 0이 된다면 해당 변수는 선형회귀분석 모형에서 무의미한 변수가 됩니다. 선형회귀분석에서 각 변수들($X$ 변수)에 대한 귀무가설은 계수가 0이라는 것입니다. 아래의 실습에서 보게 될 p-value는 바로 이 귀무가설에 대한 p-value입니다. 따라서 어떤 변수의 p-value가 유의수준보다 작다면 귀무가설을 기각하여 해당 변수의 계수가 0이 아니므로 회귀모형에서 유의미하다는 결론을 내릴 수 있습니다.
이제 예제 데이터로 선형회귀분석의 네 가지 기본가정을 어떻게 확인하고 분석을 진행하는지 알아보겠습니다.
R에서 datasets 패키지에 있는 iris 데이터를 쓸 것입니다.
전체 코드는 다음과 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
library(datasets)
library(car)
library(lmtest)
data <- iris[, -5]
str(data)
fit <- lm(Sepal.Length ~ ., data = data)
### 회귀분석 가정 확인
# 선형성, 등분산성, 정규성
plot(fit)
shapiro.test(fit$residuals)
# 독립성
vif(fit)
dwtest(fit)
### 회귀분석 결과 확인
summary(fit)
|
cs |
plot(fit)을 실행하면 차례로 plot을 볼 수 있습니다.
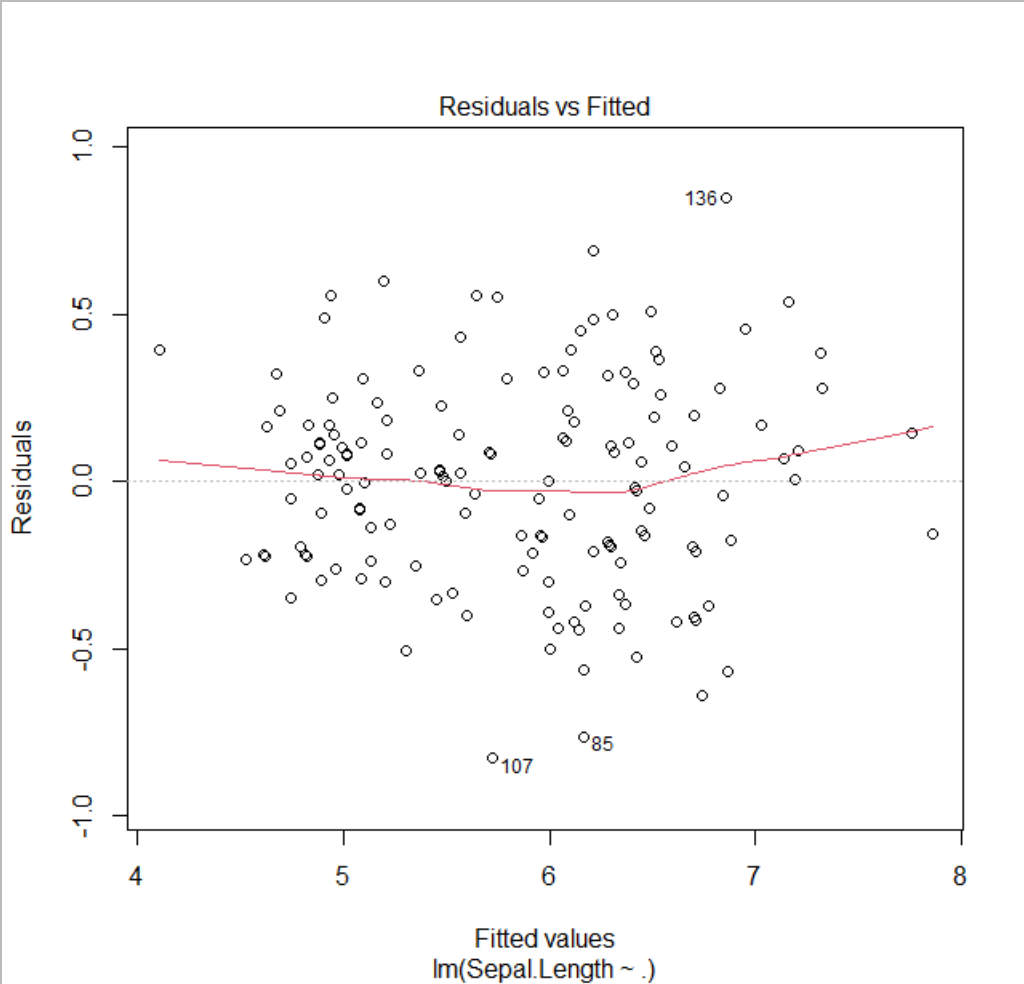
어떤 규칙성을 보이지 않는 것을 통해 등분산성 가정을 잘 만족하는 것으로 보입니다. 가장 이상적인 것은 빨간색 선이 Residuals = 0.0 인 직선을 그리는 것입니다.
이어서 Normal Q-Q Plot을 볼 수 있습니다.
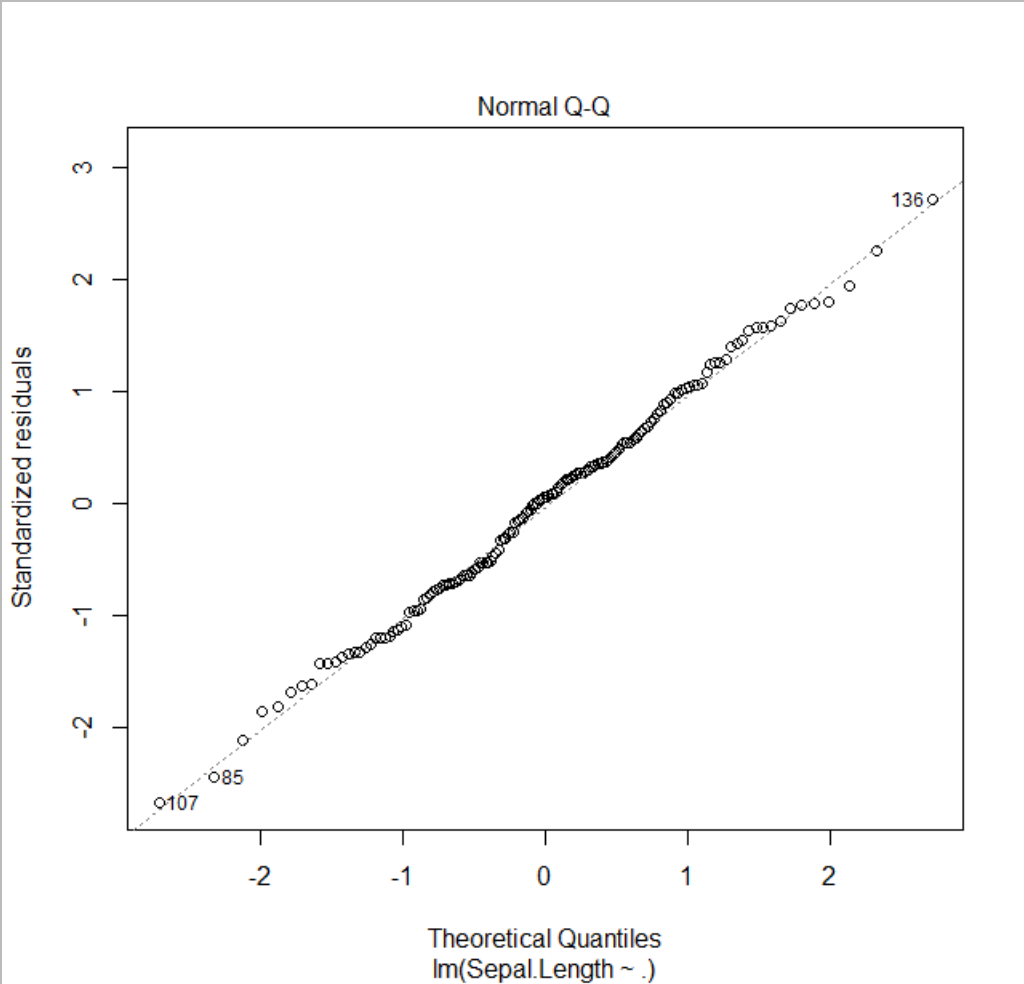
점들이 대각선 상에 잘 배치한 것을 통해 정규성을 잘 만족하는 것을 확인할 수 있습니다.
Shapiro-Wilk 검정으로도 확인해볼까요?
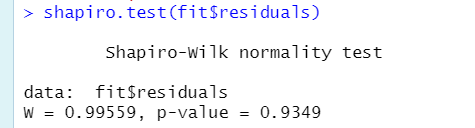
Shapiro-Wilk 검정의 귀무가설은 "데이터가 정규분포를 따른다" 입니다. 따라서 p-value가 높게 나왔으므로 해당 데이터는 정규분포를 잘 따른다고 결론내릴 수 있겠네요.
출처: kkokkilkon.tistory.com/175, www.statology.org/linear-regression-assumptions/,
'Statistics (R)' 카테고리의 다른 글
| (R) Odds ratio 메타분석 실습 (코드 리뷰) (0) | 2022.02.03 |
|---|---|
| Odds ratio & Confidence interval 계산 방법 (0) | 2021.10.22 |
| Calibration Plot 설명 (0) | 2021.08.11 |
| (Statistics, R) 기술적 통계분석 루틴 (1) : 범주형 종속변수 (0) | 2020.11.25 |
| (R) rread_csv 파라미터 정리 및 parsing failure 해결 방법 (0) | 2020.08.26 |



