| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Machine Learning
- deep learning
- Gradient Tree Boosting
- Back-propagation
- XGBoost
- Gradient Boosting Machine
- data science
- Explainable AI
- lime
- Today
- Total
Kicarussays
[논문리뷰/설명] RETAIN: An interpretable predictive model for healthcare using reverse time attention mechanism 본문
[논문리뷰/설명] RETAIN: An interpretable predictive model for healthcare using reverse time attention mechanism
Kicarus 2022. 2. 27. 09:23안녕하세요!
이번에 살펴볼 논문은 카이스트 최윤재 교수님께서 쓰신 RETAIN입니다.
RETAIN은 환자의 병원 방문과 관련된 데이터(진단, 처방, 검사, 수술 등)가 모두 있는 EHR 데이터를 활용하여, 가장 질환에 영향을 많이 미친 방문 시기가 언제인지, 어떤 진단, 처방 등이 질환에 영향을 많이 미쳤는지 설명하는 Interpretable AI 알고리즘입니다.
논문링크: https://proceedings.neurips.cc/paper/2016/hash/231141b34c82aa95e48810a9d1b33a79-Abstract.html
RETAIN: An Interpretable Predictive Model for Healthcare using Reverse Time Attention Mechanism
Requests for name changes in the electronic proceedings will be accepted with no questions asked. However name changes may cause bibliographic tracking issues. Authors are asked to consider this carefully and discuss it with their co-authors prior to reque
proceedings.neurips.cc
시작하겠습니다!
Introduction
- EHR은 고차원의 임상적 변수(진단, 처방, 수술 등)들이 시계열로 구성된 데이터로 나타낼 수 있음
- 환자 별로 매 방문마다 기록된 임상적 변수들로 시계열 데이터 구성
- 시계열 데이터를 분석하는 데에는 RNN 계열의 모델이 좋은 성능을 보이지만 모델 자체의 복잡한 구조로 인해 해석이 어렵다는 단점이 있음
- 정확도(Accuracy)와 해석가능성(Interpretability)은 서로 trade-off 관계에 있음
- RETAIN은 2개의 어텐션 구조를 적절히 활용한 모델로, 본 연구에서는 EHR 데이터와 RETAIN을 활용하여 심부전 예측 모델을 구축하고 해석 가능한 결과를 제시
- 2개의 어텐션 구조로부터 심부전 예측에 가장 영향을 미쳤던 방문과 해당 방문 시에 기록된 변수들 중 영향력 있는 변수들이 무엇인지 제시

Methodology
EHR Structure and our Notation.
$r$개의 변수를 사용하고, 전체 $N$명의 환자들 중에서 $n$번째 환자 데이터를 활용한다고 가정해봅시다. 이 $n$번째 환자가 $T^{(n)}$번의 방문 기록이 있다고 가정하면, 해당 환자의 EHR 데이터는 다음과 같이 표현할 수 있습니다. $$(t_{i}^{(n)}, \mathbf{x}_{i}^{(n)}) \in \mathbb{R} \times \mathbb{R}^r, i = 1, \cdots, T^{(n)}$$
여기서 $t_{i}^{(n)}$은 방문 시점(visit-level)에 대한 변수를 의미하고, $\mathbf{x}_{i}^{(n)}$는 해당 시점의 임상적 변수(variable-level)를 의미합니다.
이후부터는 $(n)$은 생략하고 포스팅을 계속하겠습니다.
본 논문에서 만드는 예측모델의 목표는 각 time step $i$에 대해, $\mathbf{y}_i \in \left\{ 0, 1 \right\}^s$를 예측하는 것입니다. 예측 대상은 1개 이상이 될 수 있습니다. 따라서 $s$는 1 이상의 값을 가질 수 있습니다.
데이터 예시를 한 번 봅시다.
환자의 매 방문마다 $n$개의 medical code $\mathcal{C} = \left\{ c_1, c_2, \cdots, c_n \right\}$이 기록된다고 가정하면, 매 방문마다 기록되는 데이터는 다음과 같이 나타낼 수 있습니다. $$\mathbf{x}_i \in \left\{ 0, 1 \right\}^{|\mathcal{C}|}$$
Reverse Time Attention RETAIN
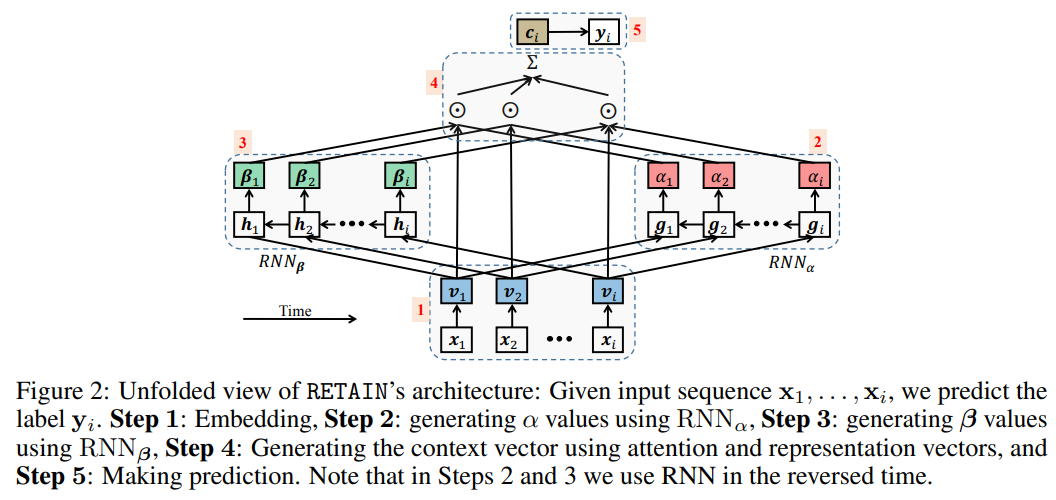

위의 구조와 수식을 바탕으로 Step별로 RETAIN을 살펴봅시다.
$i$번의 방문 기록이 있다고 가정하고 설명하겠습니다.
Step 1. Embedding
RETAIN에 데이터를 입력하기 위한 Embedding을 수행합니다.
$$\mathbf{v}_i = \mathbf{W}_{emb} \mathbf{x}_i$$
하이퍼파라미터로 설정한 embedding dimension $m$에 따라 $\mathbf{v}_i \in \mathbb{R}^m$ 입니다.
Step 2. Generating $\alpha$ values using $\text{RNN}_{\alpha}$
visit-level attention weight를 구하는 과정입니다.
$$\mathbf{g}_{i}, \mathbf{g}_{i-1}, \cdots, \mathbf{g}_{1} = \text{RNN}_{\alpha}(\mathbf{v}_{i}, \mathbf{v}_{i-1}, \cdots, \mathbf{v}_{1})$$
Embedding을 거치고 나온 $\mathbf{v}$를 $\text{RNN}_{\alpha}$에 입력하여 각 time step $i$에 해당하는 hidden layer인 $\mathbf{g}_i$를 가져옵니다. 여기서 주의할 점은 Time point가 역순으로 들어간다는 것입니다. RETAIN이 Reverse Time Attention인 이유입니다.
$$\begin{align*} e_j &= \mathbf{w}_{\alpha}^{\top} \mathbf{g}_j + b_{\alpha} \\ \alpha_1, \alpha_2, \cdots, \alpha_i &= \text{Softmax}(e_1, e_2, \cdots, e_i) \end{align*}$$
학습가능한 파라미터 $\mathbf{w}_{\alpha}, b_{\alpha}$와 $\text{RNN}_{\alpha}$의 hidden layer $\mathbf{g}$를 활용하여 visit-level attention weight $\alpha$를 구합니다. 여기서 $\alpha$는 크기가 $i$인 벡터가 됩니다. 각 $\alpha_i$는 $i$번째 방문의 중요도를 의미합니다.
Step 3. Generating $\beta$ values using $\text{RNN}_{\beta}$
variable-level attention weight를 구하는 과정입니다.
$$\mathbf{h}_{i}, \mathbf{h}_{i-1}, \cdots, \mathbf{h}_{1} = \text{RNN}_{\beta}(\mathbf{v}_{i}, \mathbf{v}_{i-1}, \cdots, \mathbf{v}_{1})$$
이번엔 Embedding을 거치고 나온 $\mathbf{v}$를 $\text{RNN}_{\beta}$에 입력하여 각 time step $i$에 해당하는 hidden layer인 $\mathbf{h}_i$를 가져옵니다.
$$\mathbf{\beta}_j = \text{tanh} \left( \mathbf{W}_{\beta} \mathbf{h}_j + \mathbf{b}_{\beta} \right)$$
학습가능한 파라미터 $\mathbf{W}_{\beta}, \mathbf{b}_{\beta}$와 $\text{RNN}_{\beta}$의 hidden layer $\mathbf{h}$를 활용하여 variable-level attention weight를 구합니다.
여기서 $\text{RNN}_{\beta}$의 hidden layer의 크기를 $q$라고 가정하여 $\mathbf{h}_{i} \in \mathbb{R}^q$일 때, $\mathbf{W}_{\beta} \in \mathbb{R}^{m \times q}$, $\mathbf{b}_{\beta}, \beta_{j} \in \mathbb{R}^m$ 입니다.
Step 4. Generating context vector using attention and representation vectors
기본 어텐션 메커니즘대로, step 2, 3의 어텐션 vector들을 사용하여 context vector를 만드는 과정입니다.
$$\mathbf{c}_i = \sum_{j=1}^{i} \alpha_j \beta_j \odot \mathbf{v}_j$$
여기서 $\odot$은 element-wise multiplication 입니다. context vector $\mathbf{c}_i \in \mathbb{R}^m$ 이 됩니다.
Step 5. Making prediction
마지막으로 우리가 원하는 결과 $\mathbf{y}_i \in \left\{ 0, 1 \right\}$^s 를 예측하는 부분입니다. 아래와 같이 단순히 fully-connected layer와 softmax 함수를 활용합니다.
$$\hat{y}_i = \text{Softmax}(\mathbf{W} \mathbf{c}_i + \mathbf{b})$$
Loss를 계산하기 위한 함수로는 아래의 cross-entropy 식을 활용하였습니다.
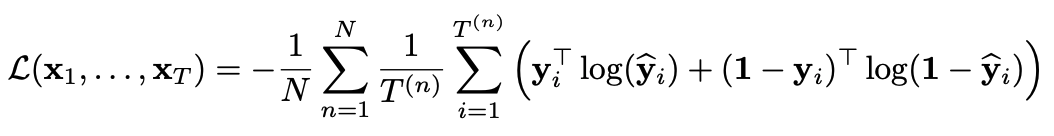
Interpreting RETAIN
몇 번째 방문이 결과 예측에 가장 많이 기여했는지는 단순히 $\alpha$를 살펴보는 것으로 알 수 있습니다. $\alpha_i$의 값이 클수록 $i$번째 방문이 결과 예측에 많은 기여를 했다고 볼 수 있는 것입니다.
하지만, 각 임상적 변수들의 기여도를 해석하는 것은 아직까지는 직관적으로 보이지 않습니다. step 3의 $\text{RNN}_{\beta}$에서, $j$번째 방문에 대한 어텐션 vector $\beta_j \in \mathbb{R}^m$는 embedding 과정을 거친 상태로 나왔기 때문에 그대로 사용할 수 없습니다.
RETAIN은 모든 $\mathbf{x}$의 변수들 $x_{1, 1}, \cdots, x_{1, r}, \cdots, x_{i, 1}, \cdots, x_{i, r}$의 변화량의 따른 결과 벡터 $\mathbf{y}$의 변화량을 분석함으로써, 모든 임상적 변수들의 기여도를 계산합니다. 어떤 메커니즘으로 이 과정이 이루어지는지 살펴봅시다.
우리는 지금 $\mathbf{x}_1, \cdots, \mathbf{x}_i$를 활용하여 예측 결과에 대한 확률벡터인 $\mathbf{y}_i$를 구하려고 합니다.

$\mathbf{c}_i$는 context vector입니다. step 4에서 살펴봤었습니다. 여기서 context vector $\mathbf{c}_i$를 치환하여 아래와 같이 쓸 수 있습니다.

우리는 $\mathbf{v}_j = \mathbf{W}_{emb} \mathbf{x}_j$ 인 것을 알고 있습니다. 따라서 Embedding 벡터에 해당하는 $\mathbf{v}_j$를 풀어서 아래와 같이 쓸 수 있습니다.

결국 $j$번째 방문에서 $k$번째 임상적 변수 $x_{j, k}$에 대한 다항식으로 확률벡터 $\mathbf{y}_i$를 나타낼 수 있습니다. 따라서 각 $x_{j, k}$의 계수에 해당하는 $$\alpha_{j} \mathbf{W} \left( \beta_j \odot \mathbf{W}_{emb} \left[:,k \right] \right)$$를 결과 예측에 대한 변수들의 기여도(Contribution Coefficient)로 볼 수 있는 것입니다.
Experiments
결과적으로 단순히 RNN만을 사용한 것과 성능은 비슷하지만, 해석가능하다는 점에서 RETAIN의 우수성을 알 수 있습니다.
RETAIN은 아래와 같이 결과에 대해 어떤 변수가 유의했는지 시각적으로 표현할 수 있습니다.

HF (Heart Failure) 진단에 가까워질수록 유의한 정도가 증가하고, Skin Disorder 등 HF와 관련이 없는 변수들보다 Cardiac dysrhythmia 등 직접적인 연관이 있는 변수들이 더욱 높은 기여도를 보이는 것을 확인할 수 있습니다.
Conclusion
RETAIN은 RNN과 어텐션 메커니즘을 적절히 활용하여 성능과 설명력, 두 마리 토끼를 모두 잡은 모델입니다. EHR 뿐만 아니라 영상, 생체신호 데이터 등 다양한 비정형 의료데이터를 적용해볼 수 있는 방안을 고민해보면 좋을 것 같습니다.
감사합니다!



