| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- lime
- Back-propagation
- Explainable AI
- Machine Learning
- data science
- Gradient Boosting Machine
- Gradient Tree Boosting
- deep learning
- XGBoost
- Today
- Total
Kicarussays
[논문리뷰/설명] DeepLIFT: Learning Important Features Through Propagating Activation Differences 본문
[논문리뷰/설명] DeepLIFT: Learning Important Features Through Propagating Activation Differences
Kicarus 2021. 9. 30. 22:15이번 논문은 딥러닝 인공신경망 모델로부터 Feature Importance를 뽑아내는 합리적인 기법을 연구하여 DeepLIFT 라는 방법을 제시한 논문입니다. 이전 포스팅에서 SHAP을 다뤄봤는데요, SHAP을 DeepLIFT에 적용하여 Feature Importance를 추출할 수도 있습니다. 이 방법은 많은 설명가능 인공지능 연구들에 사용되고 있고, 현장에서도 이미 배포된 패키지들을 활용하여 업무/연구에 활용되고 있습니다. 이 논문은 포스팅을 하고 있는 2021년 9월 30일 기준으로 1482회 인용되었습니다. 이제 시작해보겠습니다!
논문 링크: http://proceedings.mlr.press/v70/shrikumar17a
Abstract
Summary of DeepLIFT
- Backpropagation을 활용하여 특정 input의 기여도(contribution)를 확인
- 각 뉴런들의 activation을 "reference activation"과 비교하고 그 차이를 contribution score로 할당
- Positive, Negative Contribution에 서로 다른 방법 적용
- Score는 Single backward pass로 계산하여 효율성 제고
- 결과는 MNIST, simulated genomic 데이터로 검증
Introduction / Previous Work
Introduction
본 논문에서는 DeepLIFT가 다른 Blackbox 설명 모델과의 차별점을 두 가지를 제시합니다. Abstract 부분에서도 기술했지만, reference를 설정하여 비교를 통해 변수중요도를 산출하고, Positive / Negative contribution에 대해 개별적인 방법을 적용합니다. 그리고 reference 비교를 통해서, 기존 방법들이 gradient가 0이거나 불연속일 때 발생하는 문제들을 방지할 수 있다고 언급합니다. 이후 기술할 내용에서 reference 비교가 구체적으로 어떻게 이런 문제들을 방지하는지 살펴볼 것입니다.
Previous Work
딥러닝 모델로부터 변수중요도를 할당하는 이전의 방법은 무엇이 있었는지 살펴봅시다.
1. Perturbation-Based Forward Propagation Approaches (순전파 기반 접근)
이 방법은 Input에 변화를 주고, 그 변화에 따라 output 또는 다름 layer가 어떻게 변하는지 관찰하는 방법입니다. 아주 단순하고 직관적인 방법이지만 계산 효율성이 떨어지고, contribution이 포화상태일 때 중요도가 무시될 수 있다고 논문에서 언급하고 있습니다. 이게 무슨 뜻인지 살펴보기 위해 아래 이미지를 한 번 봅시다.

Input에 해당하는 $i_1, i_2$가 각각 1일 때, $i_1$ 또는 $i_2$를 0으로 감소시키면, output에 변화가 없습니다 ($i_1 + i_2$가 2에서 1로 감소). 따라서 실제로 $i_1 + i_2 < 1$인 구간에서는 input값의 변화에 따른 output의 변화를 감지할 수 있기 때문에 contribution을 산출할 수 있지만, 그 외의 구간에서는 변화를 감지할 수 없고, gradient 또한 0으로 유지되는 것을 확인할 수 있습니다 (gradient가 0이면 아무리 input이 변한다고 해도 output에 변화가 없음).
2. Backpropagation-Based Approach (역전파 기반 접근)
순전파 기반 접근방식과 달리, 역전파 기반 접근은 어떤 중요한 signal을 output 뉴런으로부터 전파시킵니다. 그렇게 input 뉴런까지 전파된 signal을 파악하여 contribution을 산출합니다. 순전파 기반 접근법은 원하는 output의 변화를 감지할 때까지 input을 계속해서 변화시켜야 하지만, 역전파 기반 접근은 사용자가 보고자 하는 변화를 output에 발생시키고, 그에 대한 input의 변화를 분석하기 때문에 계산 측면에서 큰 이득을 볼 수 있습니다. DeepLIFT는 이러한 역전파 기반 접근 방식을 차용합니다.
이러한 역전파 기반 접근 방식들에는 많은 기존 연구들이 있습니다. 하지만 기존 연구들은 ReLU와 같은 비선형의 활성함수(activation function)가 모델에 있으면, 오해의 소지가 있는 importance score를 산출할 수 있습니다. 그 예시를 아래 그림으로 한 번 살펴봅시다.

bias를 -10으로 가지고 있는 ReLU 함수를 생각해봅시다. 그림에서 확인할 수 있듯이, 그래디언트와 그래디언트 $\times$ input값이 불연속이 되고, 이로 인해 importance score가 급격하게 높아져 합리적이지 못한 결과를 산출할 수 있습니다.
DeepLIFT는 Fig 1, 2에서 제시한 기존 방법들의 문제들을 효과적으로 다룰 수 있습니다. 이제 DeepLIFT가 어떻게 작동하는지 살펴봅시다.
The DeepLIFT Method
Philosophy
DeepLIFT는 "reference" 개념을 차용합니다. reference input은 사용자가 해결하고자 하는 문제에서 "중립적"(default or neutral)인 instance로 결정하게 됩니다. reference input 선정 과정 또한 밑에서 다뤄보도록 하겠습니다.
먼저 reference input $(x_1^0, x_2^0, \cdots)$이 모델 $f$를 통과하고 나온 reference output을 $$t^0 = f(x_1^0, x_2^0, \cdots)$$ 으로 둡시다. 그리고 임의의 input $(x_1, x_2, \cdots)$에 대하여 $t = f(x_1, x_2, \cdots)$로 두고, reference와의 차이를 $$\Delta t = t - t^0$$ 라고 합시다.
이제 DeepLIFT는 $\Delta x_i$에 contribution score(기여도) $C_{\Delta x_i \Delta t}$를 할당하고, 이 contribution score는 다음과 같은 식을 만족합니다. $$\sum_{i=1}^{n} C_{\Delta x_i \Delta t} = \Delta t \tag{1}$$
본 논문에서는 이 (1)번 식을 summation-to-delta 식으로 부릅니다. 잘 기억해둡시다. 각 $x_i$에 할당된 contribution score를 모두 더하면 $\Delta t$가 되는 것이죠.
Fig 1 문제 해결
만약 딥러닝 모델의 그래디언트가 0이더라도 $(\frac{\partial t}{\partial x_i} = 0)$, 각 $C_{\Delta x_i \Delta t}$는 0이 아닐 수 있습니다. 왜냐하면 reference와의 차이에 해당하는 값이기 때문에, 그래디언트가 0인 것과는 관계없이 contribution score가 결정되는 것이죠.
이러한 DeepLIFT의 특징은 앞서 Fig 1에서 보았던 문제를 해결할 수 있는데요, 적절한 reference를 설정하면 gradient가 0이 되더라도 합리적인 contribution score를 산출할 수 있습니다. 그래디언트가 0으로 유지됨으로 인해 변수 중요도가 상실되는 문제를 컨트롤 할 수 있는 것이죠.
Fig 2 문제 해결
마찬가지로, Fig 2의 문제는 적절한 reference를 설정하여 연속적인 contribution score를 산출하여 합리적인 결과를 낼 수 있습니다. Fig 2에서 빨간 화살표로 표시된 difference-from-reference의 경우, input의 변화에 따라 안정적인 contribution score의 변화를 나타내는 것을 볼 수 있습니다.
DeepLIFT가 어떻게 기존 방법들의 문제를 컨트롤하는지 살펴보았으니, 이제 contribution score를 계산하기 위해 필요한 몇 가지 정의들을 살펴봅시다.
Multiplier and the Chain Rule
Input 뉴런 $x$와 difference-from-reference $\Delta x$, Target 뉴런 $t$와 difference-from-reference $\Delta t$에 대하여, contribution 계산을 위한 multiplier $m_{\Delta x \Delta t}$를 다음과 같이 정의합니다.
$$m_{\Delta x \Delta t} = \frac{C_{\Delta x \Delta t}}{\Delta x} \tag{2}$$
이 multiplier의 모양은 $x$의 변화에 따른 $t$의 변화량에 대한 식인 $\frac{\partial t}{\partial x}$와 유사한 것을 볼 수 있습니다. 따라서 이 multiplier를 미적분학에서 사용하는 chain rule의 컨셉에 대입해 볼 수 있습니다.
(Chain rule for multiplier)
$$m_{\Delta x_i \Delta t} = \sum_{j} m_{\Delta x_i \Delta y_j} m_{\Delta y_j \Delta t} \simeq \sum_{j} \frac{\partial y_j}{\partial x_i} \frac{\partial t}{\partial y_j} = \frac{\partial t}{\partial x_i} \tag{3}$$
multiplier에 적용된 chain rule을 활용하여, 우리는 아래와 같은 Theorem을 증명할 수 있습니다. 그리고 이 Theorem을 증명함으로써, 인공신경망 모델의 모든 뉴런의 multiplier 값을 산출할 수 있다는 결론에 이를 수 있습니다.
Theorem 1. summation-to-delta를 만족하는 $C_{\Delta x_i \Delta y_j}$, $C_{\Delta y_j \Delta t}$에 대하여, $C_{\Delta x_i \Delta t}$도 summation-to-delta를 만족한다.
$proof.$

$x_i$가 input layer의 노드들에 해당하고, $t$가 output layer의 노드, $y_j$가 hidden layer의 노드라고 한다면, 역전파 과정을 통해서 모든 노드들에 해당하는 multiplier를 구할 수 있습니다.
Defining the Reference
DeepLIFT에서는 reference를 선정하는 과정이 매우 중요합니다. 본 논문에서 reference를 선정한 방식을 한 번 살펴봅시다.
- MNIST 데이터: 모든 input이 0인 검은색 바탕 데이터를 reference로 두고 있습니다. 이 검은색 바탕인 reference input과 그로부터 산출된 reference output을 다른 데이터들과 비교하는 것이죠.
- DNA 서열 데이터: A, T, G, C 알파벳들로 이루어진 DNA 서열 데이터의 경우, 각 염기의 빈도에 따라 무작위로 만든 서열을 reference input으로 설정하였습니다.
- CIFAR10 데이터: 원래 이미지에서 흐릿한(blurred) 이미지를 만들어 각 input의 reference로 설정하였습니다.
대체로, 실제 input에서 나올 수 없는 형태의 input을 reference로 설정하고 있는 것을 확인할 수 있습니다.
Separating Positive and Negative Contributions
DeepLIFT는 contribution을 positive, negative 요소로 나눕니다. 이는 아래와 같이 표현될 수 있습니다.
$$\begin{align*} \Delta y &= \Delta y^{+} + \Delta y^{-} \\ C_{\Delta y \Delta t} &= C_{\Delta y^{+} \Delta t} + C_{\Delta y^{-} \Delta t} \end{align*}$$
간단하게 표현되어 있지만, 앞으로 DeepLIFT가 실제로 Contribution score를 산출하는 과정에서 이렇게 요소를 나눈 것이 어떻게 유용하게 쓰이는지 볼 수 있을 것입니다.
이제 DeepLIFT를 수행하기 위한 모든 준비가 끝났습니다.
Rules for Assigning Contribution Score
Contribution score를 산출하기 위한 3가지 규칙이 있습니다.
- Linear Rule
- Rescale Rule
- RevealCancel Rule
이 규칙들과 Chain rule을 활용하여 모든 input의 contribution을 합리적으로 찾을 수 있습니다.
하나씩 살펴보도록 합시다!
1. The Linear Rule
Linear Rule은 비선형성 요소(ReLU, tanh, sigmoid 등)를 제외한 Dense/Convolutional layer에 적용됩니다. $y$를 선형함수 $y=b+\sum_{i} w_i x_i$ 라고 합시다. 그럼 $\Delta y = \sum_{i} w_i \Delta x_i$으로 표현할 수 있습니다.
이제 $\Delta y$의 positive, negative 부분을 아래와 같이 정의합니다.


이후에 $\Delta y$에 대한 contribution을 아래와 같이 정리할 수 있습니다.

최종적으로 multiplier들은 $m_{\Delta x_{i}^{+} \Delta y^{+}} = m_{\Delta x_{i}^{-} \Delta y^{+}} = 1 \left\{ w_i \Delta x_i > 0 \right\} w_i$, $m_{\Delta x_{i}^{+} \Delta y^{-}} = m_{\Delta x_{i}^{-} \Delta y^{-}} = 1 \left\{ w_i \Delta x_i < 0 \right\} w_i$ 입니다. (multiplier의 정의를 적용하면 간단히 도출할 수 있습니다)
여기서 contribution score를 propagate하는 과정에서, $\Delta x_i$가 0이라면, 실제로 해당 변수가 중요한 변수더라도 중요도가 output으로 전달되지 않을 것입니다. 이런 문제를 방지하기 위해 $\Delta x_i = 0$일 때는 $$m_{\Delta x_{i}^{+} \Delta y^{+}} = m_{\Delta x_{i}^{+} \Delta y^{-}} = m_{\Delta x_{i}^{-} \Delta y^{+}} = m_{\Delta x_{i}^{-} \Delta y^{-}} = 0.5w_i$$
로 설정합니다.
여기까지 봤을 때 저는 Linear Rule이 Dense, Convolution 등의 layer에서 비선형성 activation 함수를 제외한 영역에서 multiplier들을 계산하기 위한 규칙인 것은 이해가 됐지만, 구체적인 계산 과정을 이해하기가 참 어려웠습니다. 계산 과정을 살펴보기 위해, 논문의 supplement에서 제시한 Dense layer에 적용한 Linear Rule 예시를 한번 봅시다. $X$ 다음 스텝에 $Y$가 있고, 그 사이의 weight tensor인 $W$에 대하여, $\Delta Y = \text{matrix_mul} (W, \Delta X)$로 표현됩니다.

이 식에서 $\odot$는 행렬을 elementwise로 곱한다는 기호입니다. 이 예시를 이해하기 위해서 Chain rule을 떠올려 봅시다. $m_{\Delta X \Delta t} = \sum_{j} m_{\Delta X \Delta y_j} m_{\Delta y_j \Delta t}$ 에서, $\Delta X$를 positive, negative 부분으로 나누어 식을 구성하였습니다. 각 matrix_mul에 해당하는 부분은 $\sum_{j} m_{\Delta X \Delta y_j} m_{\Delta y_j \Delta t}$이 되고, 최종적으로 postivie, negative 부분들을 계산 값을 모두 합쳐서 뒤의 step인 $Y$의 multiplier로부터 이전 step인 $X$의 multiplier들을 구한 것입니다.
여기까지 Linear Rule이 contribution score를 산출하기 위한 multiplier 계산에 어떻게 활용되는지 예시를 통해서 알아보았습니다. 이어서, DeepLIFT가 비선형적 요소(ReLU, tanh, sigmoid 등의 activation 함수)로부터 contribution score를 계산하는 과정에서 어떤 규칙이 적용되는지 살펴봅시다.
2. The Rescale Rule
activation 함수로 들어오는 input은 하나의 값입니다. 예를 들어 activation 함수 $f$와 input $x$, output $y$에 대하여, $y = f(x)$로 표현할 수 있죠. 또한 input값이 하나이니, summation-to-delta 식으로부터 $\sum C_{\Delta x \Delta y} = C_{\Delta x \Delta y} = \Delta y$, $m_{\Delta x \Delta y} = \frac{\Delta y}{\Delta x}$로 표현할 수 있습니다.
Rescale rule은 $\Delta y^{+}, \Delta y^{-}$를 다음과 같이 정의합니다.

그리고, 이로부터 다음과 같은 결론을 얻을 수 있습니다.

본 논문에서는, multiplier 계산 과정에 있어서 $x \to x^0$인 경우에 multiplier 대신 gradient를 사용한다고 언급하고 있습니다. multiplier의 분모에 해당하는 $\Delta x$가 너무 작아지면, 값이 불안정하게 산출되는 문제를 방지하기 위해서 입니다.
Rescale rule은 Fig 1, Fig 2에서 제시한 문제들을 효과적으로 다룰 수 있습니다. 다시 해당 그림들을 봅시다.

왼쪽 그림은 특정 구간에서 중요도를 전파할 수 없다는 문제를 표현하고 있고, 오른쪽 그림은 bias가 있는 비선형 activation함수가 있는 경우에 중요도가 급격하게 높아져 합리적이지 못한 결과를 낼 수 있다는 문제를 표현하고 있습니다.
Fig 1. 의 경우 문제가 되었던 구간인 $i_1 + i_2 > 1$을 봅시다. reference가 $i_{1}^{0} = i_{2}^{0} = 0$일 때, $\Delta h = -1, \Delta y = 1$이고 multiplier $m_{\Delta h \Delta y} = \frac{\Delta y}{\Delta h} = -1$ 입니다. output $y$에 대한 gradient가 0이지만, Rescale rule을 적용하면 multiplier가 -1 값을 유지하고, 이를 통해 중요도를 문제 없이 전파할 수 있는 것이죠. (논문에는 $\frac{dy}{dh} = 0$ 이라 gradient가 0 이라고 기술되어 있는데, 이 부분은 잘 이해가 안되는 것 같습니다.. $dh$가 항상 0이어서 분모가 0인데 어떻게 정의한 것일까요?)
Fig 2. 의 경우 reference를 $x^{0} = y^{0} = 0$으로 정의하고, $x = 10 + \epsilon$으로 둔다면, $\Delta y = \epsilon$이고, $m_{\Delta x \Delta y} = \frac{\epsilon}{10 + \epsilon}$, $C_{\Delta x \Delta y} = \Delta x \times m_{\Delta x \Delta y} = \epsilon$으로 계산됩니다. gradient는 급증하였던 반면에, multiplier는 안정적으로 계산되는 것을 확인할 수 있습니다. DeepLIFT는 bias 자체를 중요도에 부여하지 않습니다.
이번에는 Rescale rule로 어떻게 비선형 activation 함수에서 multiplier를 계산하는지 살펴보았고, 이 과정을 통해서 기존 방법들의 문제(Fig 1, Fig 2)를 어떻게 다루는지 살펴보았습니다. 이제 마지막 규칙이자 가장 중요한 규칙인 RevealCancel rule에 대해서 살펴봅시다.
3. The RevealCancel Rule
먼저 RevealCancel rule이 적용되는 문제가 무엇이 있는지 살펴봅시다.
(논문에서 $dy$로 쓰여진 부분은 $do$로 오타인 것으로 보입니다)

지금 보는 그림은 $i_1, i_2$ 중에서 최솟값을 취하는 문제입니다. 둘 중에 최솟값을 취하는 문제이니 당연히 $i_1, i_2$변수 모두 중요도가 동일하게 산출되어야 할 것입니다. 그런데 reference를 $i_1 = i_2 = 0$으로 두고, 이 문제에 Rescale rule을 적용하면 $i_1$ 또는 $i_2$ 둘 중 하나는 contribution score가 0으로 산출됩니다. 왜 이런 문제가 발생하는지 한 번 살펴봅시다.
- reference: $i_1 = i_2 = h_1 = h_2 = o = 0$
- $\Delta i_1 = i_1, \Delta i_2 = i_2, \Delta h_1 = h_1 = i_1 - i_2, \Delta h_2 = h_2 = \max(0, h_1), \Delta o = o = i_1 - h_2$
$\begin{align*} C_{\Delta i_1 \Delta o} &= \Delta i_1 m_{\Delta i_1 \Delta o} \\ &= i_1 \times m_{\Delta i_1 \Delta o} \\ &= i_1 \times (1 + m_{\Delta i_1 \Delta o}) \\ &= i_1 \times (1 + m_{\Delta i_1 \Delta h_1} m_{\Delta h_1 \Delta o}) \\ &= i_1 \times (1 + m_{\Delta i_1 \Delta h_1} m_{\Delta h_1 \Delta h_2} m_{\Delta h_2 \Delta o}) \\ &= i_1 \times \left( 1 + 1 \times \frac{\max(0, i_1 - i_2)}{i_1 - i_2} \times -1 \right) \\ &= i_1 \times \left( 1 - \frac{\max(0, i_1 - i_2)}{i_1 - i_2} \right) \end{align*}$
$\begin{align*} C_{\Delta i_2 \Delta o} &= \Delta i_2 m_{\Delta i_2 \Delta o} \\ &= i_2 \times \frac{\max(0, i_1 - i_2)}{i_1 - i_2} \end{align*}$
$i_1, i_2$ 둘 중 하나는 target $o$에 대하여 contribution score를 0으로 갖게 됩니다. 실제로는 두 변수 모두 결과값에 영향을 주는 변수이지만, 조건에 따라 한 변수만 영향이 있다고 결론이 나오게 되는 것이죠. 그래서 이러한 문제를 다루기 위해 RevealCancel rule을 제안하는데, 아래와 같이 $\Delta y^{+}, \Delta y^{-}$를 정의합니다.

$\Delta y^{+}, \Delta y^{-}$를 이렇게 정의하고, Fig 3. 의 문제에서 contribution score를 산출하면 각각
- $C_{\Delta i_1 \Delta o} = 0.5(i_1 + \max(0, i_1 - i_2))$
- $C_{\Delta i_2 \Delta o} = 0.5(i_1 - \max(0, i_1 - i_2))$
으로 산출됩니다. 우리가 원하는, 모든 조건에서 두 변수가 모두 영향력이 있다는 결론을 도출할 수 있습니다.
Results
MNIST
MNIST 데이터셋은 숫자 부분에 해당하는 픽셀이 1에 가까운 값(흰색)을 가지고, 그 외의 바탕 부분은 0의 값을 가집니다. DeepLIFT를 MNIST 데이터셋을 활용하여 평가하는 방식에 대해 살펴볼텐데요, 먼저 논문에서 평가 결과로 제시한 이미지를 봅시다.
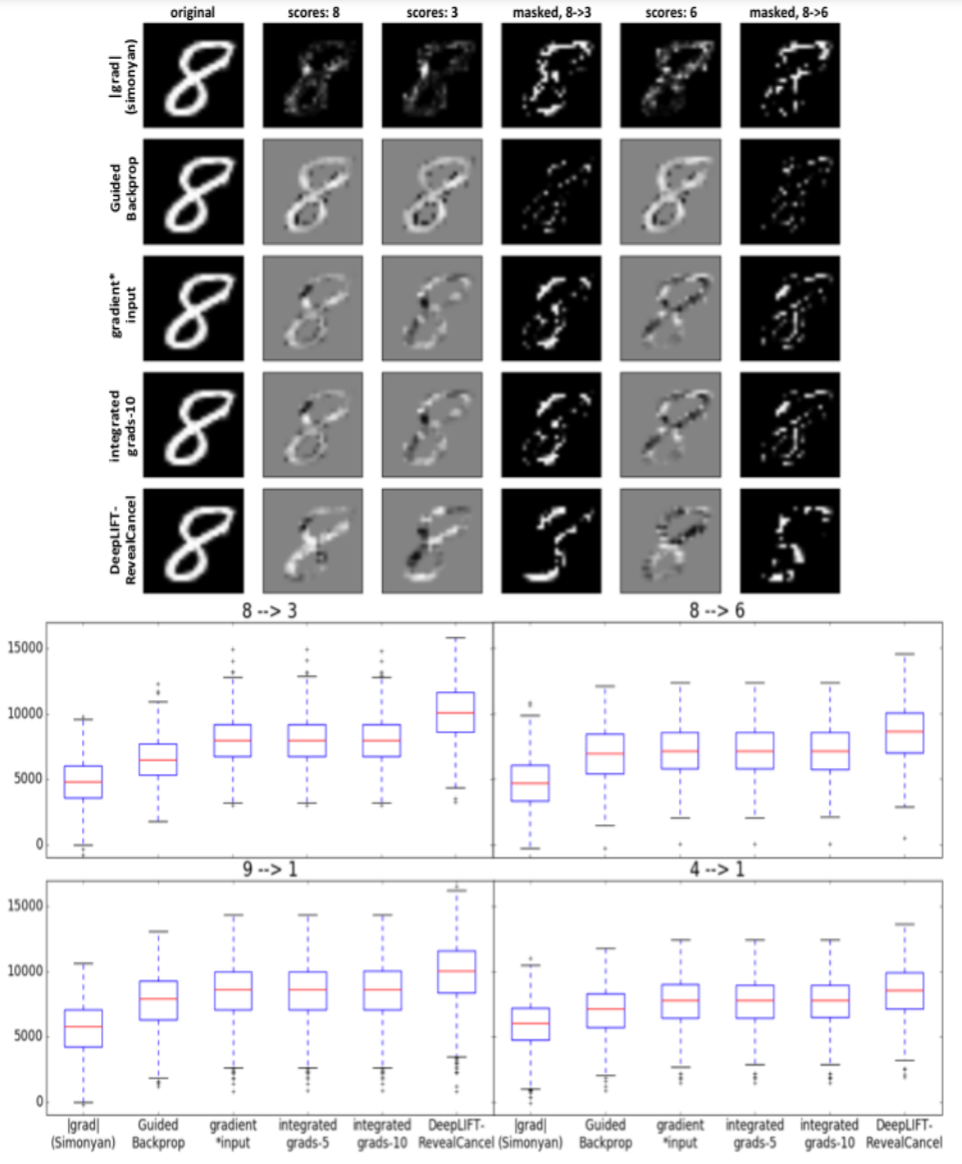
전 이 그림을 아무리 쳐다봐도 무슨 의미인지 정확하게 파악하기가 어려웠습니다.. 그래서 결국 저자가 실험을 위해 작성한 코드를 깃허브에서 다운받아서 한 줄씩 보다 보니 파악이 되었네요ㅠ 평가 과정은 아래와 같습니다.
(깃허브 링크: https://github.com/kundajelab/deeplift)
- 평가 과정 -
- reference input: 모든 픽셀이 0의 값을 가짐 -> 검은 바탕의 이미지
- original_class $c_o$, target_class $c_t$ 선정 (e.g. original: 8 / target: 3)
- class가 8인 이미지들을 추출하고, prediction값 추출
- class가 8인 이미지 개수가 $k$개라고 하면, MNIST 모델에 prediction은 $k \times 10$의 행렬임.
Cross-entropy loss 함수를 사용하였다고 가정) - 각 이미지의 prediction은 크기가 10인 벡터이고, 각 벡터의 $n$번 째 값은 class $n$에 대한 contribution으로 볼 수 있음
- class가 8인 이미지 개수가 $k$개라고 하면, MNIST 모델에 prediction은 $k \times 10$의 행렬임.
- 각 prediction의 original(8), target(3)에 대한 각각의 contribution(prediction 행렬의 8, 3번째 column)을 추출하고, 8번재 column에서 3번째 column을 뺌. 이것을 original-log-odds라고 표현
- original-log-odds는 크기가 $k$인 벡터가 되고, 모든 요소는 양수(positive)가 됨
- 이유: class가 8인 이미지를 추출했으므로, 8번째 column의 contribution이 3번째 보다 더 클 것이기 때문
- log-odds는 original / target 에 대한 contribution의 차이로 볼 수 있기 때문에, log-odds의 정의대로 직접 나누지 않고 편의상 두 contribution을 element-wise로 뺀 것이 아닐까 생각함...
- 각 이미지로부터, prediction의 8, 3번째 값에 대한 contribution score를 계산하고 8의 contribution score에서 3의 contribution score를 뺌.
- contribution score 계산하는 방식은 기존 모델들과 DeepLIFT의 RevealCancel rule을 적용한 것들을 이용
- prediction은 크기가 10인 벡터이고, 벡터의 요소들은 각각 class에 대한 contribution임
- 각 class (본 예시에서는 8, 3)에 대한 input의 contribution score를 계산할 수 있음
- contribution score 행렬은 이미지의 크기와 동일한 28*28임
- 8, 3에 대한 contribution score를 이미지로 띄운 것이 위의 이미지에서 2, 3번째 열에 해당함.
- 흰색에 가까울수록 contribution score가 높은 픽셀
- 해당 이미지들의 바탕이 회색인 이유는 이미지 자체에 정규화 작업을 진행하였기 때문임
- 여기서 8에 대한 contribution score 행렬과 3에 대한 contribution score 행렬을 뺀 것은, 모델이 input 이미지를 각각 8, 3이라고 예측하는데 기여한 부분의 차이를 의미함. 이에 대한 이미지가 4번째 열에 해당함.
- 논문에서는 이를 $S_{x_{i} \text{diff}} = S_{x_i c_o} - S_{x_i c_t}$로 표현함
- 각 이미지로부터 $S_{x_{i} \text{diff}}$의 값 상위 20%인 픽셀을 지우고(erased image), 4번에서 original-log-odds를 구한 것과 동일하게 new-log-odds를 산출한 후 original-log-odds - new-log-odds = log-odds-difference를 계산
- 이 log-odds-difference를 boxplot으로 그린 것이 이미지의 boxplot
결국 log-odds-difference값이 클수록 contribution score가 해석력이 높다고 볼 수 있습니다. 왜냐하면,
- 기존 이미지에서 8로 판단하는데 기여한 픽셀들이 3으로 판단하는데 기여하지 않고
- erased 이미지에서 3으로 판단하는데 기여한 픽셀들이 8로 판단하는데 기여하지 않을 때
- log-odds-difference값이 커지기 때문입니다.
본 논문과 supplement에는 DNA 서열 데이터와 CIFAR10 데이터를 활용하여 DeepLIFT의 성능을 검증하는 내용도 있으니, 한 번 살펴보면 좋을 것 같습니다.
Conclusion & My opinion
DeepLIFT는 새로운 방식으로 딥러닝 모델에 Importance score를 부여하는 방법을 제안했습니다. Fig 1, Fig 2 를 통해 알 수 있는 기존 방법론들의 문제를 효과적으로 해결하였고, backpropagation 방식을 차용하여 합리적으로 딥러닝 모델로부터 변수 중요도를 산출하였습니다. 개인적으로, DeepLIFT 전반에 활용되는 multiplier의 chain rule이 인상깊었는데요, multiplier가 편미분의 비율과 유사한 컨셉인 것을 바탕으로 미적분학의 chain rule을 활용하여, 본 논문에서 정의한 summation-to-delta 개념을 연쇄적으로 증명한 부분이 가장 좋았던 것 같습니다.
한편, 일전에 포스팅했던 SHAP 논문은 DeepLIFT를 활용한 새로운 설명 방법론을 제시합니다. 다음 포스팅에서는 DeepLIFT와 Shapley value를 결합한 Deep SHAP이 어떻게 작동하는지 살펴보도록 하겠습니다.



