| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Back-propagation
- deep learning
- Explainable AI
- data science
- XGBoost
- Gradient Tree Boosting
- lime
- Gradient Boosting Machine
- Machine Learning
- Today
- Total
Kicarussays
[논문리뷰/설명] LIME: "Why Should I Trust You?" Explaining the Predictions of Any Classifier 본문
[논문리뷰/설명] LIME: "Why Should I Trust You?" Explaining the Predictions of Any Classifier
Kicarus 2021. 8. 2. 10:34딥러닝을 비롯한 여러 방법론들은 우수한 성능을 보이며 각광받고 있지만, 그런 방법론들에는 늘 "Blackbox"라는 꼬리표가 달려 있습니다. 아무래도 모델의 복잡성이 증가할수록 성능은 향상되지만 설명력이 낮아진다는 점에서 그렇겠죠.
이번에 소개할 논문은 이런 블랙박스 모델들을 인간의 언어로 설명하는 방법론에 대한 논문입니다. 제가 포스팅을 하고 있는 2021년 8월 기준으로 6105회(;;;) 인용되었네요. 2016년에 발표된 논문임을 감안하면 정말 엄청난 인용수입니다.
이 논문을 쓰신 Marco Tulio Ribeiro 교수님은 마이크로소프트 리서치에서 근무 중이고, 박사 학위를 받았던 워싱턴 대학에서 겸임교수를 하고 있다고 하네요. 대단한 이력을 가지고 있으신 만큼 이 논문도 정말 신선하고 놀라운 방법론들을 소개하고 있습니다. 이제 시작해보겠습니다!
논문 링크: https://arxiv.org/abs/1602.04938
"Why Should I Trust You?": Explaining the Predictions of Any Classifier
Despite widespread adoption, machine learning models remain mostly black boxes. Understanding the reasons behind predictions is, however, quite important in assessing trust, which is fundamental if one plans to take action based on a prediction, or when ch
arxiv.org
Introduction & The Case For Explanations
머신 러닝 기법들은 많은 성과를 거두고 있지만, 아무리 성능이 좋은 모델이라도 사용자가 납득할 수 있는 설명을 제시하지 못한다면 모델을 차용하기 어려울 것입니다. 특히 사람의 건강과 생명이 걸린 의료현장에서는, 의사가 납득할 수 있도록 설명가능하고 신뢰할 수 있는 모델만이 사용될 수 있습니다.
여기서 저자는 신뢰(Trust)에 대하여 두 가지 정의를 내립니다.
- 개별 예측값에 대한 신뢰(Trusting a prediction)
- 모델에 대한 신뢰(Trusting a model)
본 논문에서는 이렇게 정의한 두 가지 신뢰 문제를 해결하기 위해 설명(Explanation)을 제시하는 알고리즘을 제안합니다. 개별 예측값에 대한 설명을 제시하는 LIME(Local Interpretable Model-agnostic Explanations), 모델에 대한 설명을 돕기 위해 대표적인 Instance 집합을 구성하는 SP-LIME(Submodular Pick - LIME)입니다.
이 두 알고리즘을 설명하기에 앞서, 그렇다면 설명은 어떤 방식으로 제시되는지 살펴볼 필요가 있습니다.
개별 예측값에 대한 설명은, 어떤 모델이 Output을 제시했을 때, 이 Output이 어떤 Input의 영향을 받아 제시되었는지에 대한 설명입니다. 논문에서는 아래 그림으로 개별 예측값에 대한 설명을 표현합니다. 독감을 예측하는 모델에서, "환자(Input)가 독감(Output)이다"라는 결론을 냈을 때, LIME은 어떤 Input에 가중치를 두고 독감이라는 결론을 내렸는지 말해줍니다.

모델에 대한 설명은, 전체 모델이 어떤 Feature들을 중요하게 여기는지에 대한 설명입니다. 이를 간단히 표현하자면, 어떤 두 모델 중 하나를 선택하고자 할 때, 전체적으로 더 합리적인 설명들을 제시하는 모델을 선택한다는 것입니다.

위 그림에서는 두 알고리즘 중에서 어떤 알고리즘을 선택할지 고민 중인 상황입니다. 무신론자를 찾는 모델에서, 알고리즘 1이 더 합리적으로 변수의 유의성을 보여주고 있는 것을 볼 수 있습니다. 만약 성능의 차이가 크지 않다면, 인간의 입장에서 합리적인 근거로 결론을 도출하는 알고리즘을 선택하게 되겠죠.
이어서 저자는 LIME을 비롯한 설명 모델(Explainer)들이 갖추어야 할 세 가지 요건들을 제시합니다.
1. Interpretability
인간이 이해할 수 있는 방식으로 설명이 제시되어야 한다는 것입니다.
만약 Random Forest처럼 수백, 수천 개의 트리를 구성하거나, 몇천 개의 변수를 활용하는 회귀분석 등은 인간의 언어로 설명이 어려울 것입니다. 저자는 중요한 변수를 선별하여 설명하는 등의 작업이 필요하고, 이 Interpretabillity의 개념은 설명 대상(Target Audience)에 따라 달라질 수 있다고 말합니다.
2. Local Fidelity
모델이 제시하는 설명이 적어도 국소적으로는 합리적(Locally Faithful)이어야 한다는 것입니다.
이 개념은 전체적으로는 중요한 Feature(Global Fidelity)가 개별 Prediction을 예측할 때는 중요하지 않을 수 있다는 사실에서 기인한 것입니다. 예를 들어, 흰 쌀밥, 주스, 바나나 등 당뇨 환자들이 피해야 하는 대표적인 음식들이 있습니다. 하지만 어떤 당뇨환자의 상태가 나빠졌다고 해서 저런 음식들만이 영향을 미치지는 않았을 것이고, 더 영향을 준 국소적인 영향이 있을 것이며, Explainer는 이 국소적인 영향(Local Fidelity)을 제시해줄 수 있어야 한다는 것입니다. 이런 Local Fidelity를 잘 보여주는 아래 그림을 논문에서 제시하고 있습니다.

3. Model-agnostic
Explainer는 해석의 대상이 되는 모델의 종류와 관계없이 설명을 제시할 수 있어야 한다는 것입니다.
Decision Tree, Logistic Regression 등 그 자체로 해석이 가능한 모델들이 있습니다. 하지만 우수한 성능을 자랑하는 최신 모델들은 우수한 성능만큼 복잡하고 인간의 언어로 설명이 매우 어렵습니다. 이러한 모델의 복잡성에 구애받지 않고 설명을 제시할 수 있어야한다는 것이 Explainer의 마지막 요건입니다.
지금까지 신뢰(Trust)의 정의, Explainer가 제시하는 설명의 형태, Explainer가 갖추어야 할 세 가지 요건에 대해 살펴보았습니다. 이제 본격적으로 LIME 알고리즘에 대해서 살펴봅시다.
Local Interpretable Model-agnostic Explanation(LIME)
LIME의 목표는 분류기(Classifier)에서 Locally Faithful한 설명을 제시하는 것입니다.
3.1 Interpretable Data Representation
해석가능한 설명은 인간이 이해가 가능한 형태이어야 합니다. 따라서
3.2 Fidelity-Interpretability Trade-off
모델은 복잡할수록 성능이 좋은 편이고, 이 부분에서 성능과 복잡도 사이에는 Trade-off가 있습니다. LIME에서 Trade-off 관계를 활용하여 가장 좋은 Explainer를 찾습니다. 이 과정이 수식으로 어떻게 나타나는지 봅시다.
Explainer
모든
이제 우리가 설명하고자 하는 대상이 되는 모델
설명하고자 하는 Instance
최종적으로
본 논문에서 LIME을 통해서 생성되는, Instance
설명하고자 하는 모델
이 식이 어떻게 구체적으로 계산되는지는 3.4에서 다룰 것입니다.
3.3 Sampling for Local Exploration
Introduction에서 소개했던 Explainer의 세 가지 요건 중 Local Fidelity를 떠올려봅시다. 당뇨에 좋지 않은 음식이라고 해서, 어떤 당뇨환자가 항상 그 음식으로 인해 문제가 생겼다고 볼 수는 없고, 다른 국소적인(Local) 원인이 있을 수 있습니다. 따라서
먼저
LIME에서는
이제 이
3.4 Sparse Linear Explanation

LIME은 Instance
(논문의 알고리즘에는 Lasso가 밑에 부분에 나와있는데, 먼저 수행해주어야 하는 것으로 이해했습니다)
<LIME 작동 예시>
1. 전체 데이터 X에 대하여, Lasso Regression을 수행하고, 총
K d′ K - 3.2의 (1)번 식에서 모델의 복잡도에 따라 부여했던
Ω(g)
(K개 Feature를 먼저 선정하여 설명의 복잡도(Ω(g)
2. 이제 설명하고자 하는 모델
x′,z′ K N z′ N
3.
πx(z) x,z πx - 직관적으로
x,z f(z) g(z′)
(L - 여기서
g
4.
여기까지 LIME의 작동 원리를 살펴보았습니다. LIME은 설명하고자 하는 모델
- Blackbox 모델을 Interpretable 모델로 설명하는 과정에서, 성능이 저하될 수 있다.
- Explainer로 Linear Model을 선정할 경우, Non-linear 모델을 설명할 때 Locality 설명이 왜곡될 수 있다.
이러한 한계들은 앞으로 Explainable AI 연구에서 발전해나가야 할 부분이 될 것입니다.
Submodular Pick for Explaining Models (SP-LIME)
LIME은 개별 결과값들을 설명하는 방법입니다. 그렇다면, 두 모델 중 우수한 모델을 선정하기 위해서는 어떻게 해야할까요?
데이터의 개수가 많다면 모든 데이터의 설명을 살펴보는 것은 어려울 것입니다. 따라서 우리는 가장 모델을 잘 설명하는 대표 데이터군을 선정할 필요가 있습니다. SP-LIME은 대표 데이터군을 뽑는 알고리즘입니다.

<SP-LIME 작동 원리>
1. 모든 데이터
- LIME은 결과적으로 설명 가능한 모델
gi gi xi
2. 모든 Feature(설명 가능 모델
3. 모델의 설명력을 보기 위해 살펴볼 Instance의 개수
4. Coverage 함수
- Coverage 함수는
V - Coverage 문제는 NP-Hard 문제이기 때문에 Greedy Algorithm 방식을 차용합니다.
- 이와 같은 방식으로 모든 Feature를 Cover하는 Instance들을 뽑습니다.
결국 사용자가 살펴볼 Instance의 개수(
Simulated User Experiments
이제 LIME과 SP-LIME이 잘 작동하는지 확인하기 위해 세 가지를 검증해야 합니다.
- 설명 자체가 합당한가?
- 이 예측이 합당한가?
- 이 모델이 합당한가?
검증 방식과 결과를 살펴봅시다.
1. 설명 자체가 합당한가?
이에 대한 대답을 위해 그 자체로 설명가능한 모델 Logistic Regression, Decision Tree를 사용합니다. Decision Tree, Logistic Regression으로부터 가장 유의한 Feature 10개를 선정하고, LIME의 결과로 나온 Feature들이 이 10개의 Feature를 잘 Cover하는지 Recall(재현율)을 확인합니다.
아래 결과에서 LIME과의 비교 대상은 임의 추출(Random), Parzen(다른 방법론), Greedy입니다. 이들 중에서 LIME이 가장 좋은 결과를 보였다는 것을 말하고 있습니다.

즉, LIME이 중요하다고 선정한 Feature들과 기존 설명가능 방법론들이 선정한 Feature이 90% 이상의 재현율을 보였다는 것입니다.
2. 이 예측이 합당한가?
LIME의 예측을 믿을 수 있는지 확인하기 위해, 단계별로 살펴봅시다.
0) 설명하고자 하는 모델
- 중요하지 않은 Feature의 예시로는, 환자의 질병 유무를 판별하는 데, 환자의 휴대전화 기종 같은 Feature가 될 것입니다.
X′ U
1)
- 절대적으로 사용자가 중요하지 않다고 결정한 Feature는 예측 결과(
f(X) - 따라서
f(X),f(X′) f
2) LIME을 통해 나온
gi - 그 Feature들에는
U - 원래
gi U
3) 1, 2번에서 라벨링한 결과들을 비교하여 F1 score 측정
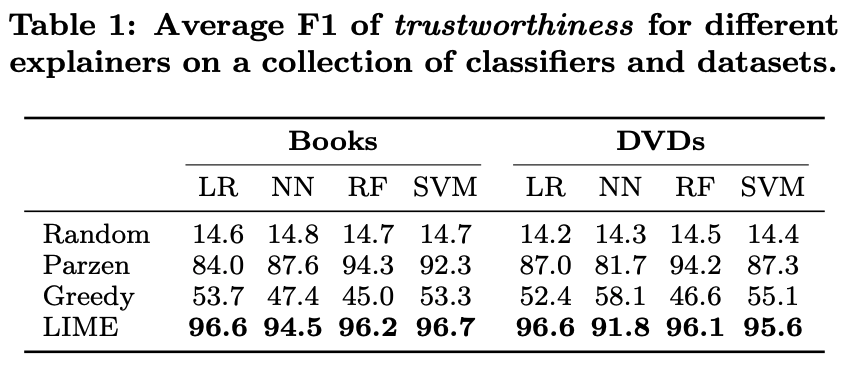
LIME으로 나온 결과는 설명 가능한 결과입니다. 하지만, 그 결과 자체를 믿을 수 없다면 의미가 없을 것입니다.
그래서 본 논문에서는 결과의 신뢰도 측정 방식을 제시하고, 원래 모델과 LIME으로 나온 결과 사이의 신뢰도를 비교합니다. 그 결과는 위의 테이블에서 확인할 수 있습니다.
3. 이 모델이 합당한가?
SP-LIME은 가장 모델을 잘 설명하는 Instance를 뽑아주는 알고리즘입니다. 이를 통해서 나온 Instance들 중에 Trustworthy한 Instance의 비율을 측정하는 방식으로 모델이 합당한지 확인합니다.
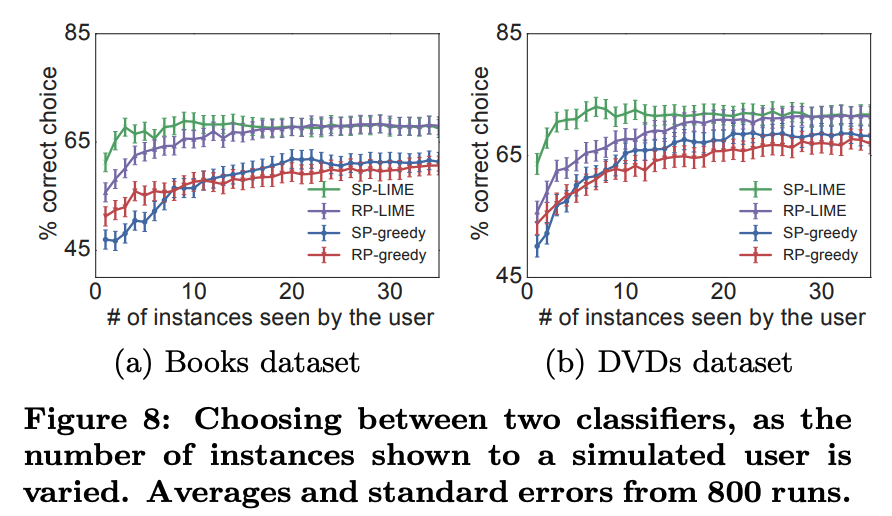
SP-LIME이 가장 우수한 결과를 나타내는 것을 확인할 수 있었습니다.
Evaluation With Human Subjects
각 데이터셋 분야의 전문가들이 직접 실험에 참가한 결과입니다. LIME과 SP-LIME을 통한 설명을 보고, 전문가들이 직접 설명의 타당성, 모델의 타당성을 평가합니다.
My Opinion
이 논문은 인공지능의 설명가능성을 상당히 잘 제시한 논문입니다. Blackbox의 한계는 모두가 알고 있었지만, 이에 대한 광범위한 해결 방법을 제시한 사람은 없었습니다. LIME, SP-LIME은 모든 분류기, 심지어 회귀기에서도 사용할 수 있습니다.
2016년에 나온 논문인 만큼, 지금은 더 많이 발전된 방법론이 제시되었을 것입니다. 이 방법들을 잘 답습하여 의료데이터에 최신 방법들을 잘 적용하면, 설명가능성의 부재로 의료현장에서 사용되지 못했던 많은 우수한 머신러닝, 딥러닝 방법론들이 날개를 펼 수 있을 것 같습니다.



