| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- data science
- Gradient Boosting Machine
- Machine Learning
- deep learning
- Explainable AI
- XGBoost
- Gradient Tree Boosting
- lime
- Back-propagation
- Today
- Total
Kicarussays
[논문리뷰/설명] LightGBM: A Highly efficient Gradient Boosting Decision Tree 본문
[논문리뷰/설명] LightGBM: A Highly efficient Gradient Boosting Decision Tree
Kicarus 2021. 12. 13. 13:44LightGBM은 예전에 한 프로젝트에서 정형 데이터 (Table 형태의 데이터) 에 여러 머신러닝 기법들을 적용해보던 중에 발견한 방법이었습니다. CPU만 사용하면서도 GPU를 쓰는 XGBoost보다 훨씬 더 빠르고, 성능도 비슷해서 놀랐던 기억이 있습니다. (LightGBM 패키지에 GPU 사용 옵션이 있긴 하지만 당시에 GPU 연동에 실패했었습니다, 나중에 다시 시도해보고 LightGBM과 GPU를 연동하는 방법을 소개하는 포스팅을 올려볼 계획입니다)
LightGBM이 어떻게 이렇게 효율적인 학습을 가능케 하는지 논문을 직접 읽어보며 정리해보았습니다.
논문 링크: https://papers.nips.cc/paper/2017/hash/6449f44a102fde848669bdd9eb6b76fa-Abstract.html
Introduction
Gradient Boosting Decision Tree?
Gradient Boosting Decision Tree (GBDT) 는 테이블 데이터에서 좋은 성능을 보이는 트리 기반 알고리즘입니다. 먼저 Decision Tree 앞부분에 왜 Gradient Boosting이 붙었는지 간단히 살펴봅시다.
1. Boosting
Boosting 기법은 매 단계를 거치며 이전 단계에서 잘 학습하지 못한 부분을 보다 집중적으로 학습 하는 방식입니다.
2. Gradient
그래디언트는 학습과정에서 손실함수를 줄이기 위한 방향을 알려주는 함수 입니다. 예를 들어, 최고차항이 양수인 2차함수의 최솟값을 찾으려면 임의의 점에서 기울기의 반대방향으로 움직여야 하는 것처럼, 그래디언트 값의 반대 방향 으로 움직여야 손실함수가 최소가 되는 지점으로 갈 수 있는 것입니다.
수식으로 예를 들어보겠습니다. 손실함수
시그마 앞의 계수
그래디언트의 -1을 곱한 값이 실제 output인
3. Gradient Boosting Decision Tree (GBDT)
Decision Tree를 만드는 과정에 Gradient Boosting을 활용하는 것입니다. 트리가 가지를 늘려가는 과정에서 Gradient를 계산하여 손실함수를 가장 큰 폭으로 줄일 수 있는 부분에서 leaf를 나눕니다 (Split). 또한 매 단계마다 이전 단계에서 잘 학습하지 못했던 데이터를 보다 집중적으로 학습하는 트리를 만듭니다.
GBDT를 만드는 과정 중에서 가장 많은 시간과 자원이 소요되는 부분은 split 지점을 찾는 부분 입니다. 해당 Feature의 모든 값을 정렬하고, 가능한 모든 split 지점 중에서 어떤 부분이 가장 잘 데이터를 분류하는지 찾아야 하기 때문입니다. 이렇게 모든 split 지점을 확인하는 것은 매우 비효율적이기 때문에, 효율적으로 GBDT를 구성하기 위해 많은 방법들이 제시되고 있습니다 (e.g. XGBoost, LightGBM, CatBoost).
LightGBM의 특징
LightGBM은 논문에서 GOSS, EFB라고 명명한 두 가지 알고리즘을 사용하는 것이 큰 특징입니다.
- GOSS: 데이터셋의 샘플 (instance) 수를 줄이는 알고리즘
- EFB: 데이터셋의 Feature 수를 줄이는 알고리즘
하나씩 살펴봅시다.
Gradient-based One-Side Sampling (GOSS)
GOSS는 데이터셋의 샘플 수를 줄이는 알고리즘 이고, 기본 가정은 instance의 gradient가 클수록 영향력이 크고 덜 학습된 insatnce라는 것입니다.
instance의 gradient가 크다는 것은, 해당 instance를 구성하는 값(element)들의 변화가 손실함수에 큰 변화를 가져올 수 있다는 것입니다. LightGBM에서는 이런 instance를 모델이 충분히 학습하지 못한 instance 라고 보고 있고, 따라서 이러한 instance를 포함하면서 데이터셋의 샘풀 수를 줄이려고 시도합니다.
GOSS가 어떻게 데이터셋의 샘플 수를 줄이는지 그 과정을 간단히 살펴봅시다. 논문에서 제시한 알고리즘은 다음과 같고, 아래에 정리하여 설명을 덧붙였습니다.

- 각 instance들의 gradient 계산 및 정렬
- gradient 상위
a×100 - 남은 instance들 중에서
b×100 1−ab
- 이 instance들은 모델이 이미 충분히 학습한 데이터지만, 데이터셋의 분포를 유지하기 위해 일부분을 포함시킵니다
1−ab - b의 값이 적을수록 큰 가중치를 곱해주게 됩니다
- 이를 통해 원래 데이터셋의 분포를 크게 변화시키지 않고 데이터셋의 크기를 줄일 수 있습니다
- 선택한 instance들로 GBDT 생성
아주 간단하고 효율적인 아이디어입니다. 트리를 학습할 때에는 각 Split 지점에 해당하는 Information gain을 모두 계산하고 가장 큰 Information gain을 갖는 지점을 Split하게 되는데, 본 논문에서는 축소한 데이터셋과 원래 데이터셋의 Information gain의 차에 Upper bound가 있다 는 것을 수학적으로 증명하는데, 축소한 데이터셋이라도 어느 수준 이상으로 차이가 발생하지는 않는다는 것입니다. 그 증명 과정을 살펴봅시다.
(트리 학습 과정에서의 Information gain에 대한 포스팅은 다음 링크에 아주 잘 설명되어 있습니다)
먼저 GBDT를 학습하는 과정 (Split 과정) 에서 얻는 information gain (variance gain) 을 아래와 같이 정의합니다.

Variance gain이라고 하는 이유는 Split 이후에 각 leaf에 분류된 데이터들이 분산이 작을수록 더 잘 분류되었다고 볼 수 있기 때문입니다. 아래 이미지로 이해할 수 있습니다.
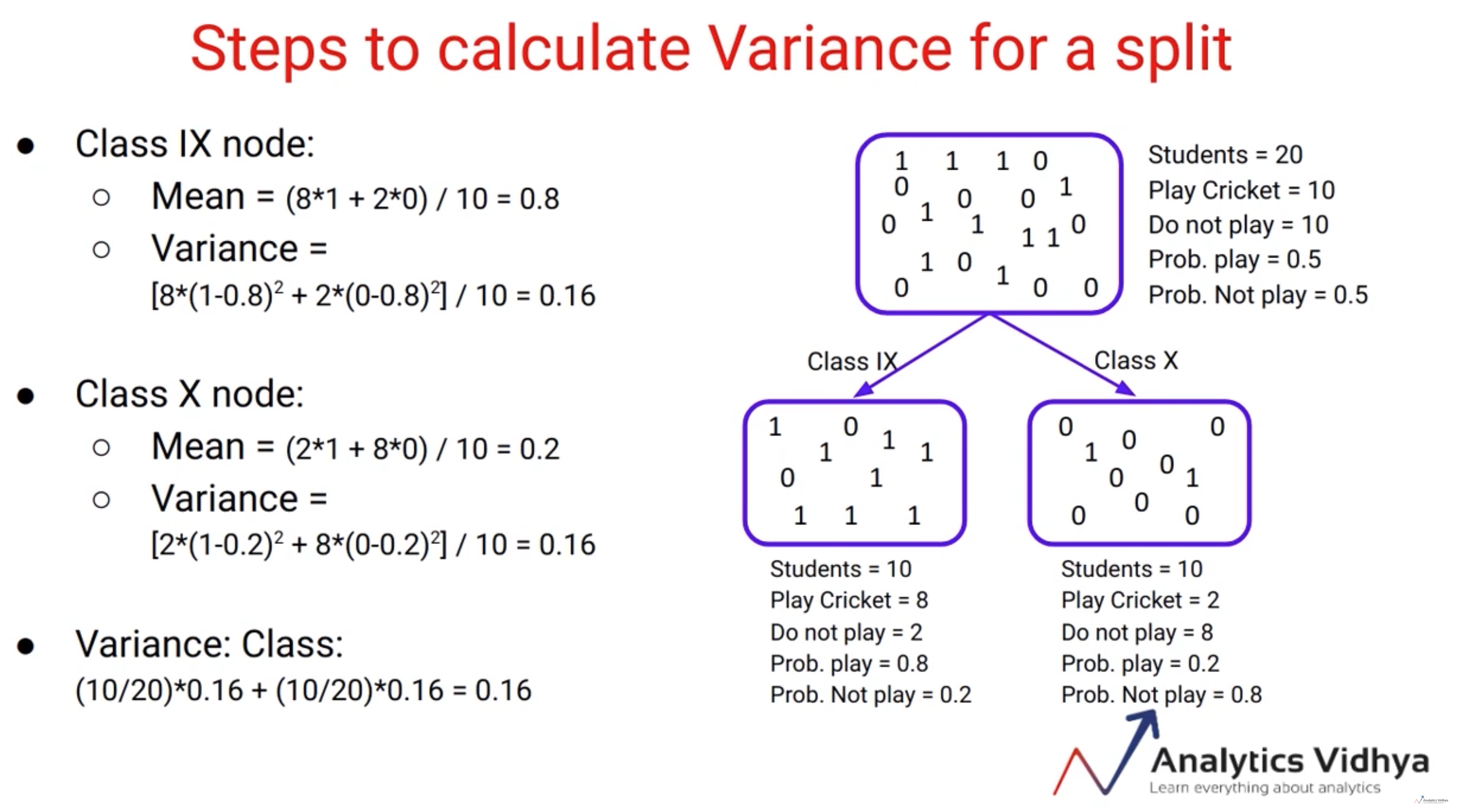
왼쪽과 오른쪽 leaf에 각각 속한 instance들이 최대한 분산이 낮을수록
산술기하평균 부등식을 통해
이어서 GOSS를 통해 축소한 데이터셋으로 계산한 variance gain
gradient 상위
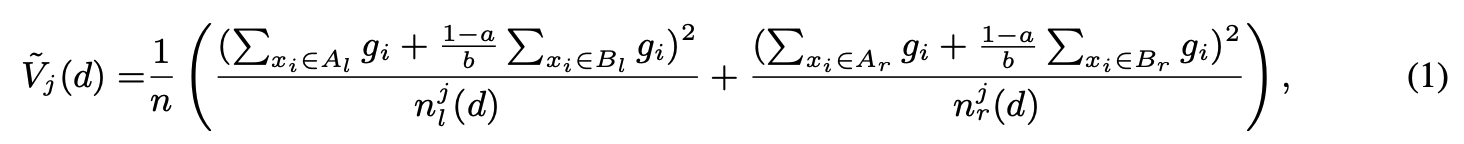
여기서
아래는 이

위의 정리를 두고, n이 커질수록, split point를 통해 instance들이 좌우 leaf에 균등하게 분리될수록 approximation error가 작아진다 고 말합니다.
논문에서는 이를
어쨌든 GOSS 알고리즘을 통해서 만든 축소된 데이터셋으로도 충분한 성능을 보일 수 있다는 것이 이 Theorem의 골자입니다.
이어서, GOSS의 일반화 성능 (generalization performance) 에 대해 살펴봅시다. GOSS를 통해 축소한 데이터셋과 모집단 데이터 사이의 variance gain의 차이를 볼 것입니다.
삼각부등식을 활용해봅시다.
앞서 Theorem 3.2 에서
Exclusive Feature Bundling (EFB)
EFB는 데이터셋의 Feature 수를 줄이는 알고리즘 입니다. 고차원의 데이터는 sparse하다는 가정 하에, 상호배타적인 변수들을 하나의 bucket으로 묶어서 Feature 수를 줄이는 방식입니다. 여기서 "상호배타적인 변수들"은 동시에 0이 아닌 값을 갖지 않는 변수들을 말합니다.
논문에서는 이렇게 상호배타적인 변수들을 묶어서 최소의 bundle 로 만드는 문제는 NP-hard이기 때문에 Greedy 알고리즘을 활용해야한다고 주장합니다. 최소 bundle 문제를 대표적인 NP-hard 문제인 그래프 색칠 문제로 환원 (reduction) 하여 NP-hard라는 것을 보입니다 (Theorem 4.1). 그래프 색칠 문제는 서로 연결된 노드를 서로 다른 색으로 칠할 때 필요한 최소한의 색깔의 개수를 찾는 문제입니다.

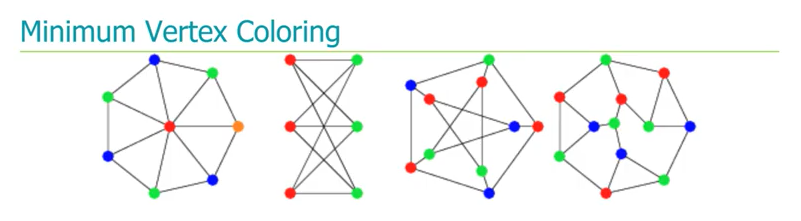
Theorem 4.1 을 요약하면 다음과 같습니다.
- 데이터셋의 각 변수들을 그래프의 Vertex로 치환
- 상호배타적이지 않은 변수들을 Edge로 연결
(상호배타적인 변수들은 서로 연결되어 있지 않으므로 같은 색으로 칠할 수 있음) - 이 그래프 색칠 문제에서 최소한의 필요한 색깔의 수는 bundle의 개수에 대응됨
여담으로 그래프 문제는 대표적인 NP-complete 문제입니다. NP-complete는 NP-hard의 부분집합이기 때문에 NP-hard라고 해도 상관은 없지만 본 논문에서는 NP-hard라고 언급하였습니다.
어쨌든 최소한의 bundle을 찾는 문제는 NP-hard 이기 때문에 다항시간 내에 이 문제를 푸는 알고리즘은 존재하지 않습니다. 따라서 Greedy 알고리즘을 통해서 이 문제에 대한 근사적인 답을 찾고자 하는 것입니다.
추가적으로, 100% 상호 배타적인 변수들은 적을 것이기 때문에, 어느정도 conflict (상호배타적이지 않은 instance의 개수) 를 허용하는 조건을 추가합니다. 이를 random polluting 이라 하고, 논문에서는 random polluting을 적용하였을 때 결과의 차이에는 Upper bound가 있다는 정리를 제시합니다 (Proposition 2.1). 저는 이 증명 과정을 잘 이해하지는 못했는데... 혹시 아시는 분이 있다면 댓글로 알려주시기 바랍니다!!! 이 정리는 결국 conflict를 허용하더라도 성능에 큰 저해는 없다는 것입니다.
이 random polluting은 파라미터
논문에서 제시한 Greedy 알고리즘을 살펴봅시다.
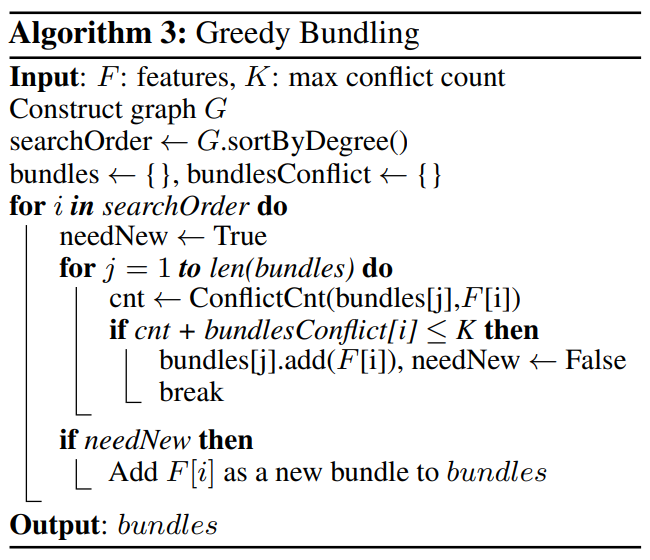
Algorithm 3 을 요약하면 다음과 같습니다.
- 변수들의 상호배타여부를 고려하여 그래프
G
- 서로 상호배타적인 변수들은 Edge로 연결되어 있지 않음
- 각 Edge의 Weight는 Edge와 연결된 두 Vertex 사이의 conflict
- 그래프의 각 Vertex들의 Degree를 계산하고, Degree의 크기에 따라 정렬
- Vertex의 Degree는 해당 Vertex에 연결된 모든 Edge들의 weight의 합
- bundle을 만들고, Degree가 큰 변수 순서대로, 나머지 다른 변수들간의 conflict 계산
- conflict의 합이 전체 데이터셋 개수
×γ×100 - bundle의 conflict 합이 기준을 넘어가면 새로운 bundle을 만들고, 모든 변수를 다 쓸 때까지 3, 4과정을 반복
여기까지 변수들을 상호배타적인 bundle로 구성하는 방법이었습니다.
이제 bundle로 구성한 변수들을 하나의 변수로 만드는 과정 (merging) 이 필요합니다. 논문에서는 아래와 같은 알고리즘으로 방법을 제시합니다.

Algorithm 4 를 요약하면 다음과 같습니다.
- bundle 내에서 기준 변수 설정
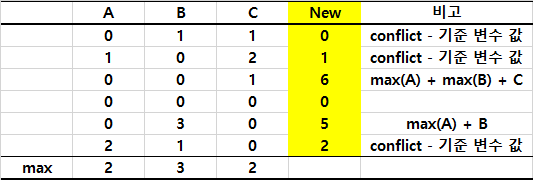
- 모든 instance에 대해서, conflict 한 경우는 기준 변수 값 그대로 가져감
- 모든 instance에 대해서, conflict가 아닌 (상호배타적인) 경우 기준 변수의 최대값 + 다른 변수 값을 취함
변수들에 해당하는 값들이 서로 겹치지 않게 기준 변수의 최댓값에 해당 변수의 값을 더해서 새로운 변수 값으로 취하는 것입니다. 아래 예시는 bundle에 3개 변수가 있을 때의 예시입니다.
Experiments
LightGBM의 최대 장점은 무엇보다 알고리즘의 수행 속도입니다. 다른 GBM 알고리즘들보다 압도적으로 빠른 수행 속도를 보입니다. 성능 또한 SOTA 알고리즘에 해당하는 XGBoost와 비슷한 수준입니다.
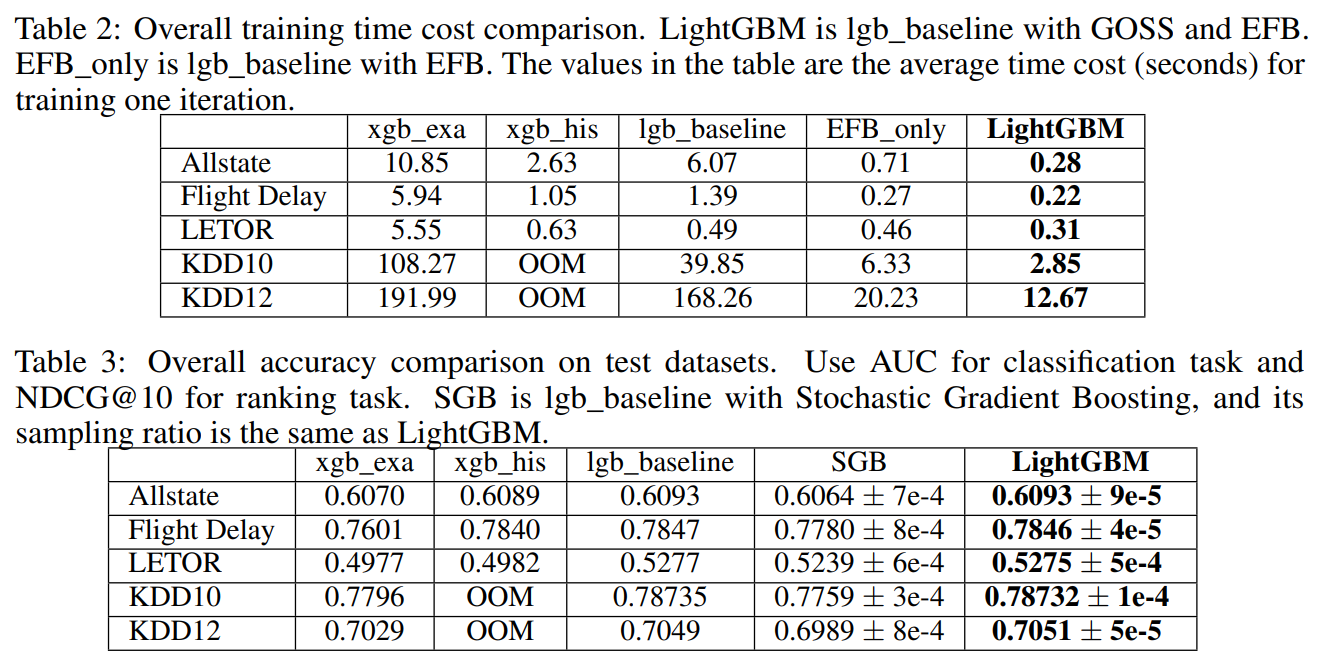
Table 2에서 LightGBM의 수행속도가 매우 빠른 것을 확인할 수 있습니다. 또한 성능 면에서도 우수합니다.
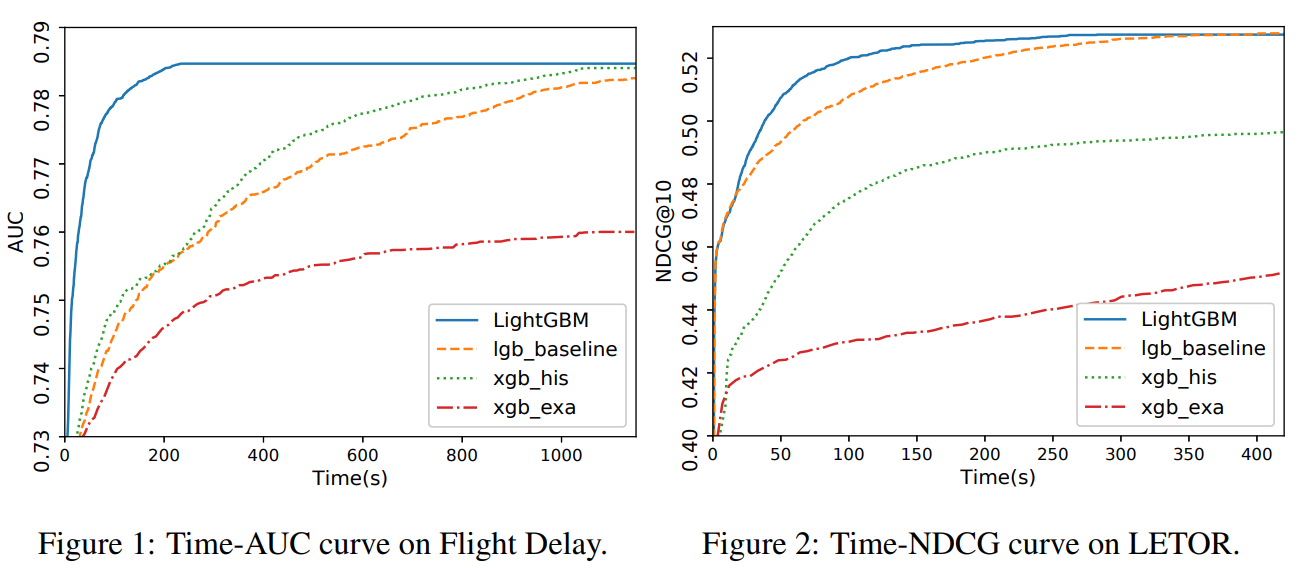
위 그래프에서는 LightGBM이 학습할 때 어떤 정확도 수준까지 다른 방법론들에 비해 매우 빨리 도달하는 것을 확인할 수 있습니다.
GOSS의 파라미터인
Conclusion
LightGBM은 GOSS, EFB라는 새로운 알고리즘을 통해서 데이터셋의 크기를 줄이고, 수행 속도를 큰 폭으로 높였습니다. 또한 수학적으로 해당 알고리즘을 사용했을 때의 손실에 Upper bound가 있다는 것을 보였고, 실험 결과도 그에 부합하는 것을 확인할 수 있었습니다.
평소에 잘 사용하던 알고리즘이 어떤 원리로 작동하는지 살펴보고, 보다 구체적이고 납득할 수 있는 이유를 바탕으로 학습하는 모델을 만드는 것은 이후의 연구들에 많은 도움이 되는 것 같습니다.
감사합니다!
참고자료
https://www.youtube.com/watch?v=4C8SUZJPlMY
'Machine Learning' 카테고리의 다른 글
| [논문리뷰/설명] Learning with Local and Global Consistency (0) | 2022.03.30 |
|---|---|
| [논문리뷰/설명] CatBoost: unbiased boosting with categorical features (1) | 2022.01.04 |
| [논문리뷰/설명] XGBoost: A Scalable Tree Boosting System (2) Weighted Quantile Sketch (0) | 2021.06.30 |
| [논문리뷰/설명] XGBoost: A Scalable Tree Boosting System (1) (0) | 2021.05.17 |



